There is a composite solid made up of a circular cylinder and on this a hemisphere is fixed. The refractive index of both the solids is μ, for a laser beam incident as shown. You are given that the radius of the hemisphere is R and the length of the cylinder is 3R/2 . calculate the final divergence of the ray . (μ=√32)

15∘
30∘
45∘
none of the above
The correct Answer is:D
Step by step video & image solution for There is a composite solid made up of a circular cylinder and on this a hemisphere is fixed. The refractive index of both the solids is mu, for a laser beam incident as shown. You are given that the radius of the hemisphere is R and the length of the cylinder is 3R/2 . calculate the final divergence of the ray . (mu=sqrt3/2) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Light is incident on the thin lens as shown in figure. The refractive index of the material of the lens is μ2. The radii of curvature of both the surfaces are R. The refractive index of the medium of left side is μ1, while that of right side is μ3. What is the focal length of the lens?

View SolutionA solid consisting of a right circular cone, standing on a hemisphere, is placed upright, in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm, the radius of the hemisphere is 2 cm and the height of the cone is 4 cm. Give your answer correct to the nearest centimetre
( Take π=317)
View SolutionA sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is r, then the volume of the cylinder is 4π r3 (b) 83π r3 (c) 2π r3 (d) 8π r3
View SolutionA solid is in the form of a right circular cylinder, with a hemisphere at one end and a cone at the other end. The radius of the common base is 3.5 cm and the heights of the cylindrical and conical portions are 10 cm and 6 cm, respectively. Find the total surface area of the solid. (Use π=22/7 )
View SolutionA horizontal ray of light is incident on a solid glass sphere of radius R and refractive index μ . What is net deviation of the beam when it emerged from the other side of the sphere?
View SolutionShow that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R√3 .
View SolutionShow that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R√3 .
View SolutionShow that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R√3
View SolutionShow that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R√3 .
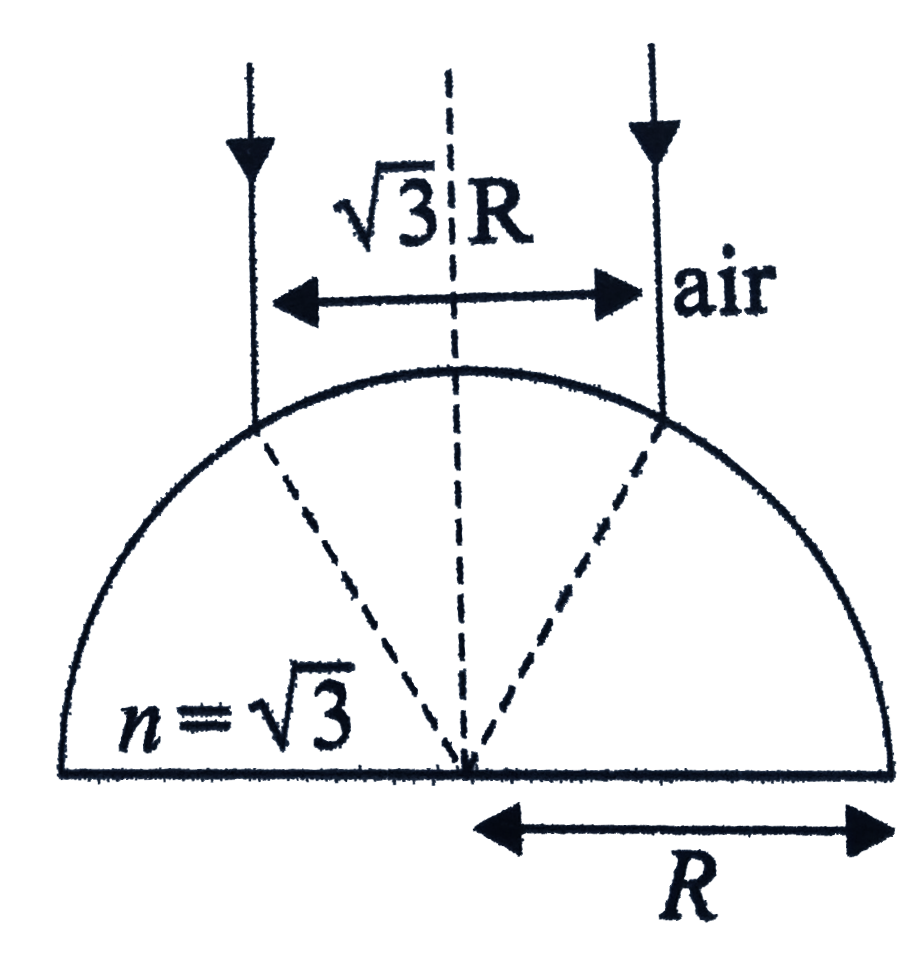
View SolutionA light beam of diameter √3R is incident symmetrically on a glass hemisphere of radius R and of refractive index n=√3 . Find radius of the beam at the base of hemisphere.
View Solution
