A bar of mass m resting on a smooth horizontal plane starts moving due to the force F=mg/3 of constant magnitude. In the process of its rectilinear motion the angle α between the direction of this force and the horizontal varies as α=as, where a is a constant, and s is the distance traversed by the bar from its initial position. Find the velocity of the bar as a function of the angle α.
The correct Answer is:v=√(2g/3a)sinα
To solve the problem step by step, we will analyze the motion of the bar under the influence of the force F=mg3 and the relationship between the angle α and the distance s.
Step 1: Understand the Forces Acting on the Bar
The bar of mass m is subjected to:
- Its weight mg acting downwards.
- The applied force F=mg3 at an angle α with the horizontal.
Step 2: Resolve the Applied Force into Components
The applied force can be resolved into two components:
- Horizontal component: Fcosα
- Vertical component: Fsinα
Step 3: Write the Equations of Motion
Using Newton's second law, we can write the equations for the vertical and horizontal directions.
Vertical Direction:
N+Fsinα=mg
Where N is the normal force.
Horizontal Direction:
Fcosα=ma
Where a is the horizontal acceleration of the bar.
Step 4: Substitute the Force
Substituting F=mg3 into the equations:
1. Vertical Equation:
N+mg3sinα=mg
Rearranging gives:
N=mg−mg3sinα=mg(1−13sinα)
2. Horizontal Equation:
mg3cosα=ma
Simplifying gives:
a=gcosα3
Step 5: Relate Acceleration to Velocity
We know that acceleration can also be expressed as:
a=dvdt=dvds⋅dsdt=vdvds
Thus, we can write:
vdvds=gcosα3
Step 6: Substitute the Angle Relation
Given that α=as, we can express cosα in terms of s:
cosα=cos(as)
So, the equation becomes:
vdvds=gcos(as)3
Step 7: Integrate the Equation
We can separate variables and integrate:
∫vdv=g3∫cos(as)ds
This gives:
v22=g3∫cos(as)ds
Step 8: Solve the Integral
The integral ∫cos(as)ds=1asin(as), so we have:
v22=g3⋅1asin(as)+C
Assuming initial conditions where v=0 when s=0, we find C=0.
Step 9: Final Expression for Velocity
Thus, we can express v2 as:
v2=2g3asin(as)
Taking the square root gives:
v=√2g3asin(as)
Final Answer
The velocity of the bar as a function of the angle α is:
v=√2g3asin(as)
The bar of mass m is subjected to:
- Its weight mg acting downwards.
- The applied force F=mg3 at an angle α with the horizontal.
The applied force can be resolved into two components:
- Horizontal component: Fcosα
- Vertical component: Fsinα
Using Newton's second law, we can write the equations for the vertical and horizontal directions.
N+Fsinα=mg
Where N is the normal force.
Fcosα=ma
Where a is the horizontal acceleration of the bar.
Substituting F=mg3 into the equations:
1. Vertical Equation:
N+mg3sinα=mg
Rearranging gives:
N=mg−mg3sinα=mg(1−13sinα)
mg3cosα=ma
Simplifying gives:
a=gcosα3
We know that acceleration can also be expressed as:
a=dvdt=dvds⋅dsdt=vdvds
Thus, we can write:
vdvds=gcosα3
Given that α=as, we can express cosα in terms of s:
cosα=cos(as)
So, the equation becomes:
vdvds=gcos(as)3
We can separate variables and integrate:
∫vdv=g3∫cos(as)ds
This gives:
v22=g3∫cos(as)ds
The integral ∫cos(as)ds=1asin(as), so we have:
v22=g3⋅1asin(as)+C
Assuming initial conditions where v=0 when s=0, we find C=0.
Thus, we can express v2 as:
v2=2g3asin(as)
Taking the square root gives:
v=√2g3asin(as)
The velocity of the bar as a function of the angle α is:
v=√2g3asin(as)
Similar Questions
If z(¯¯¯¯¯¯¯¯¯z+α)+¯z(z+α)=0, where α is a complex constant, then z is represented by a point on
View SolutionA locomotive of mass m starts moving so that its velocity varies according to the law v=a√s, where a is a constant, and s is the distance covered. Find the total work performed by all the forces which are acting on the locomotive during the first t seconds after the beginning of motion.
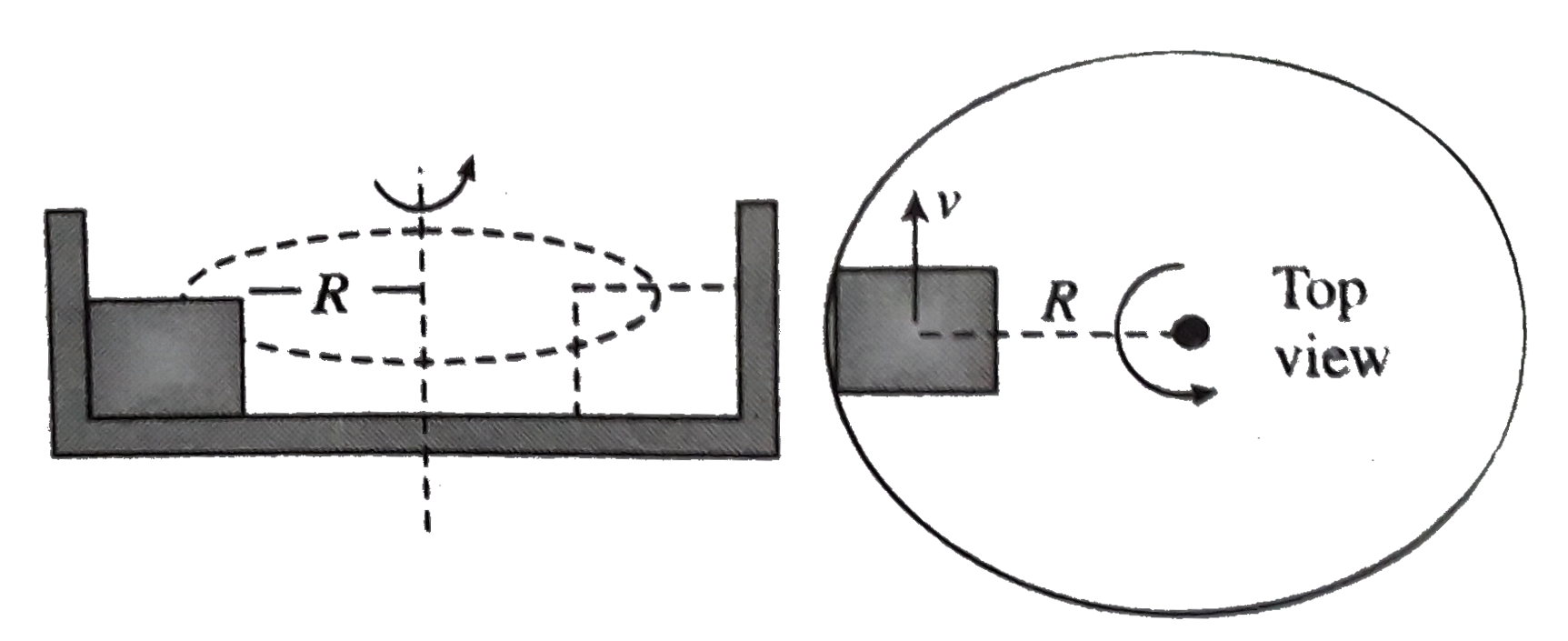
View SolutionA block of mass m is revolving in a smooth horizontal plane with a constant speed v.If the radius of the circle path is R find the total contact force received by the block
View SolutionA force F of constant magnitude acts on a block of mass 'm' and t=0,initially along positive x-direction. The direction of force F starts rotating with a constant angular velocity ω in anticlockwise sense. Then the magnitude of velocity of the block as a function of time 't' is ( initial block was at rest )
View SolutionA body of mass M is resting on a rough horizontal plane surface the coefficient of friction being equal to μ At t=0 a horizontal force F=F0t starts acting on it , where F0 is a constant find the time T at which the motion starts?
View SolutionThe kinetic energy of a particle moving along a circle of radius R depends on the distance covered S as K =α.S2, where α is a constant. Find the force acting on the particle as a function of S.
View SolutionA block of mass M is resting on a smooth horizontal plane. One end of a uniform rope of mass M4 is fixed to the block , which pulled it in the horizontal direction by applying a force F at the other ends . The tension in the middle of the rope is
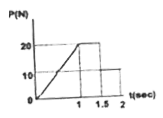
View SolutionA body of mass 6.25kg is travelling in a horizontal straight line with a velocity of 3m/ sec when a horizontal force P is applied to it at right angle to the initial direction of motion. If P varies according to the accompanying graph, remains constant in direction and is the only force acting on the body in its plane of motion,find the magnitude of the velocity of the body when t=2 sec.
View SolutionA particle of mass m starts moving from origin along a horizontal x-y plane under the influence of a force of constant magnitude F ( which is always parallel to the x-axis ) and a constraint force. The trajectory of its motion is f(x)=xx2+1. Then,
View SolutionA particle moves in a circular path such that its speed 1v varies with distance s as v=√s, where ∝ is a positive constant. Find the acceleration of the particle after traversing a distance s.
View Solution
