In an isosceles triangle ΔABC,AB=AC and ∠A=80∘. The bisector of ∠Band∠C meet at D. The ∠BDC is equal to the
90∘
100∘
130∘
80∘
The correct Answer is:C
Step by step video, text & image solution for In an isosceles triangle DeltaABC, AB = AC and /_A = 80^@. The bisector of /_B and /_C meet at D. The /_BDC is equal to the by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-III)109videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IV)35videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF25videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
Knowledge Check
- Question 1 - Select One
In △ABC ,∠A=40∘. If the bisector of ∠B and ∠C meet at a point O in the interior of the triangle, then ∠BOC is equal to:
त्रिभुज ABC में, ∠A=40∘ है |यदि कोण B तथा कोण C के द्विभाजक त्रिभुज के आतंरिक भाग में एक बिंदु O पर मिलते हैं, तो ∠BOC का क्या होगा ?A130∘B90∘C70∘D110∘ - Question 2 - Select One
In an isosceles triangle ABC,AB=AC,XY∣∣BC. If ∠A=30∘, then ∠BXY=?
A75∘B30∘C150∘D105∘ - Question 3 - Select One
In △ABC ,∠A=50∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=50∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के द्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान क्या होगा ?A70∘B65∘C55∘D40∘
In Figure, ABC is an isosceles triangle with AB=AC and m ∠ABC=500. Find m ∠BDC and ∠BEC
View SolutionIn ΔABC,AB=AC and the bisectors of ∠B and ∠C meet at a point O. Prove that BO=CO and the ray AO is the bisector of ∠A.
View SolutionIn a ΔABC, the bisectors of ext ∠B and ext ∠C meet at D. If BD>CD, then prove that AC>AB.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
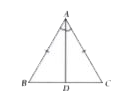
ΔADB≅ΔADCView SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
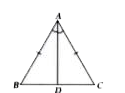
∠B=∠CView Solution

