Two circles intersect each other at the points A and B, A straight line parallel to AB intersects the circles at C, D, E and F. If CD = 4.5 cm, then the measure of EF is
1.50cm
2.25cm
4.50cm
9.00cm
The correct Answer is:C
To solve the problem, we need to find the length of EF given that CD = 4.5 cm and that the line segment CD is parallel to the line segment EF.
1. Understanding the Configuration:
- We have two circles that intersect at points A and B.
- A line parallel to AB intersects the circles at points C, D, E, and F.
2. Given Information:
- The length of segment CD is given as 4.5 cm.
3. Properties of Parallel Lines:
- Since CD is parallel to EF, and both segments are intercepted by the same two circles, we can use the property of parallel lines. This property states that if two lines are parallel and are cut by a transversal (in this case, the line connecting the points of intersection), the segments formed on the circles will be proportional.
4. Using the Perpendicular from the Centers:
- Let’s denote the centers of the circles as O1 and O2.
- If we drop perpendiculars from O1 and O2 to the line segments CD and EF, we can denote the points where these perpendiculars meet the segments as N (for CD) and M (for EF).
- By the properties of circles, the segments will be equal because the perpendicular from the center to a chord bisects the chord.
5. Setting Up the Equation:
- Since CN = NF and DN = NE (because of the perpendiculars), we can express the lengths as:
- CD = CN + DN
- EF = NE + NF
- Since CN = NF and DN = NE, we can say:
- CD = 2 * CN
- EF = 2 * NE
6. Finding the Length of EF:
- Since CD = 4.5 cm, we can conclude that:
- EF = CD
- Thus, EF = 4.5 cm.
Conclusion:
The measure of EF is 4.5 cm.
- We have two circles that intersect at points A and B.
- A line parallel to AB intersects the circles at points C, D, E, and F.
- The length of segment CD is given as 4.5 cm.
- Since CD is parallel to EF, and both segments are intercepted by the same two circles, we can use the property of parallel lines. This property states that if two lines are parallel and are cut by a transversal (in this case, the line connecting the points of intersection), the segments formed on the circles will be proportional.
- Let’s denote the centers of the circles as O1 and O2.
- If we drop perpendiculars from O1 and O2 to the line segments CD and EF, we can denote the points where these perpendiculars meet the segments as N (for CD) and M (for EF).
- By the properties of circles, the segments will be equal because the perpendicular from the center to a chord bisects the chord.
- Since CN = NF and DN = NE (because of the perpendiculars), we can express the lengths as:
- CD = CN + DN
- EF = NE + NF
- Since CN = NF and DN = NE, we can say:
- CD = 2 * CN
- EF = 2 * NE
- Since CD = 4.5 cm, we can conclude that:
- EF = CD
- Thus, EF = 4.5 cm.
The measure of EF is 4.5 cm.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)70videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)90videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XI)22videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
Two circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionIn figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that □ ABCD is cyclic.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The radius of two concentric circles are 17cm and 10cm. A straight line ABCD intersects the larger circle at the point A and D and intersects the smaller circle at the points B and C. If BC = 12 cm, then the length of AD (in cm) is :
A20B24C30D34
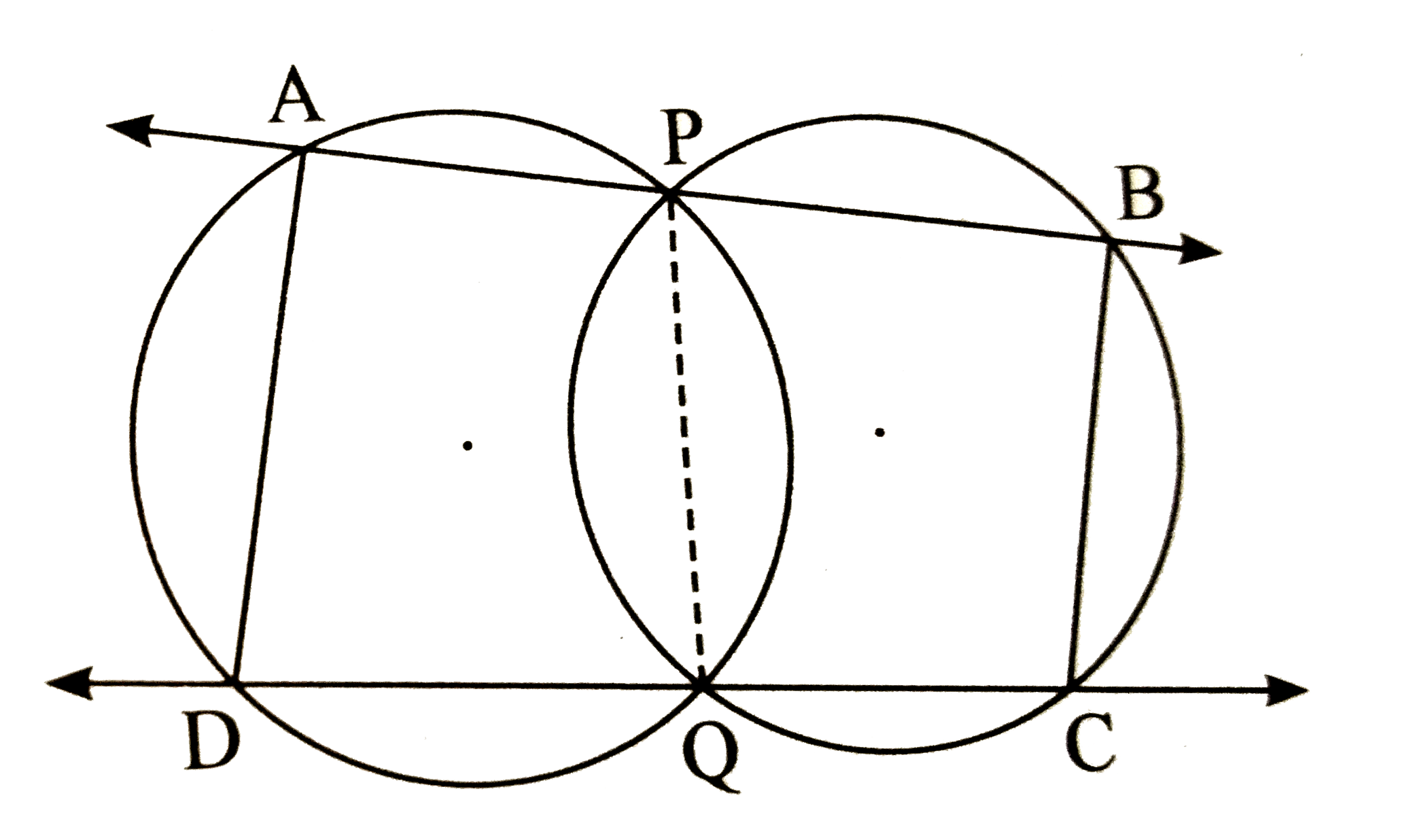
Two circles whose centres are O and O' intersect at P. Through P, a line l parallel to OO' intersecting the circles at C and D is drawn. Prove that CD=2 OO'
View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
 View Solution
View SolutionIn the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circles. Prove that PBQ is a straight line.
 View Solution
View SolutionTwo circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ACP =∠QCD.
View SolutionIn the figure, two circles with centers O and P intersect each other at points D and C. Line AB intersects the circle with centre O at points A and B and touches the circle with centre P at point E. Prove ∠ADE+∠BCE=180∘.
 View Solution
View SolutionIn the figure, two circles intersect each other at points A and B . C is a point on the smaller circle. Secant CA and secant CB of the smaller circle intersect the bigger circle at points D and E respectively then prove : seg DE ∣∣ line CF
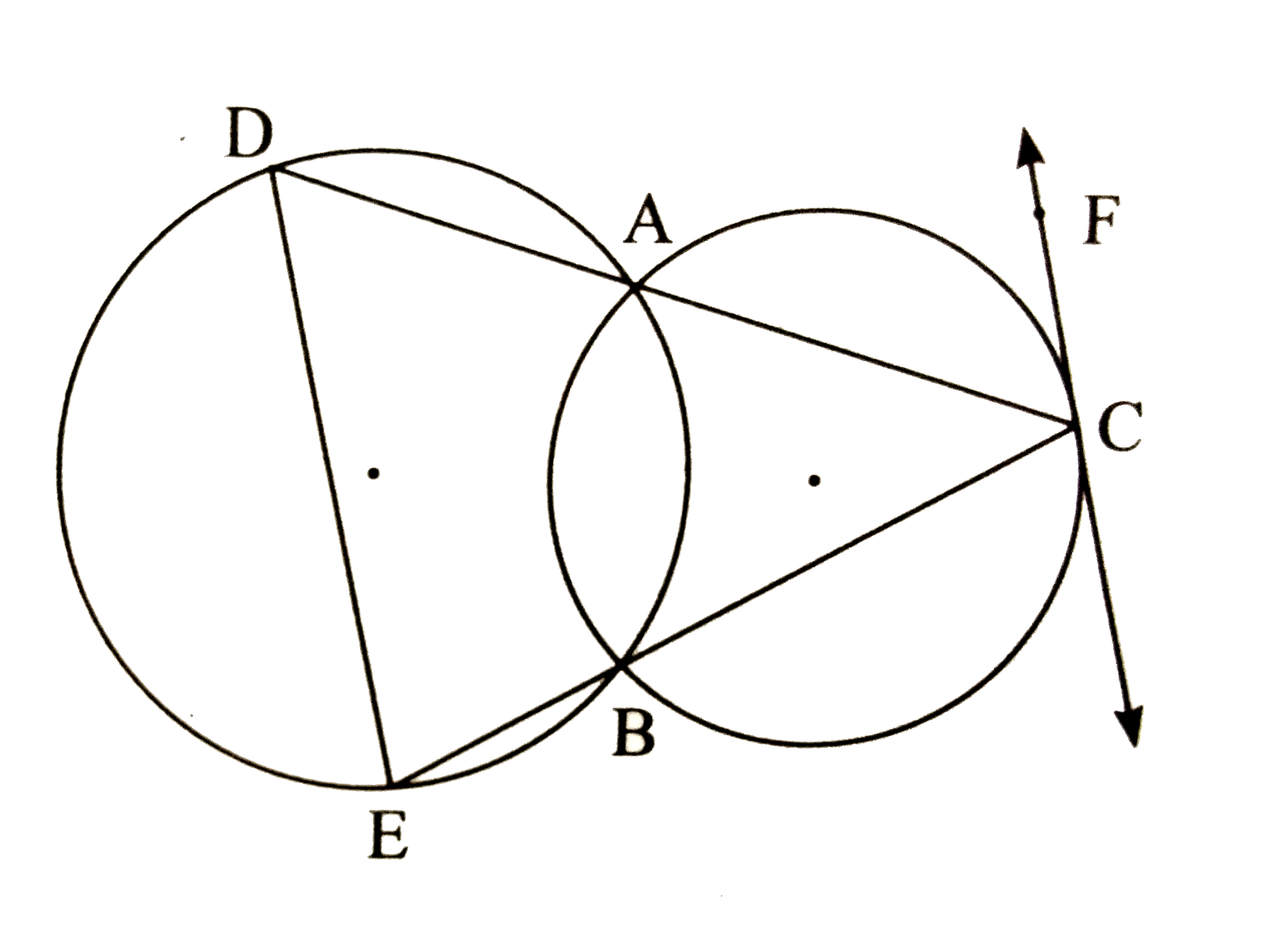 View Solution
View SolutionTwo circles intersect in A and B, and the measure of the common chord ¯¯¯¯¯¯AB = 10 cm. The line joining the centre cuts the circles in P and Q. If PQ = 3 cm, and the measure of the radius of one circle is 13 cm. Find the radius of the other circle.
View Solution

