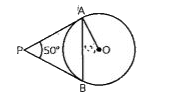
If PA and PB are two tangents to a circle with centre O such that ∠APB=80∘, then, ∠AOP=?
40∘
50∘
60∘
70∘
The correct Answer is:B
Step by step video, text & image solution for If PA and PB are two tangents to a circle with centre O such that /_APB = 80^@, then, /_AOP = ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
90 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF
25 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
90 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
Knowledge Check
If PA and PB are tangents to the circle with centre O such that ∠APB=50∘ then ∠OAB is equal to
A50∘B30∘C40∘D25∘In the given figure, if PA and PB are tangents to the circle with centre O such that ∠APB=54∘, then ∠ OAB equals
A36∘B18∘C27∘D36∘In figure, if PA and PB are tangents to the circle with centre O such that ∠APB=50∘, then ∠OAB is equal to
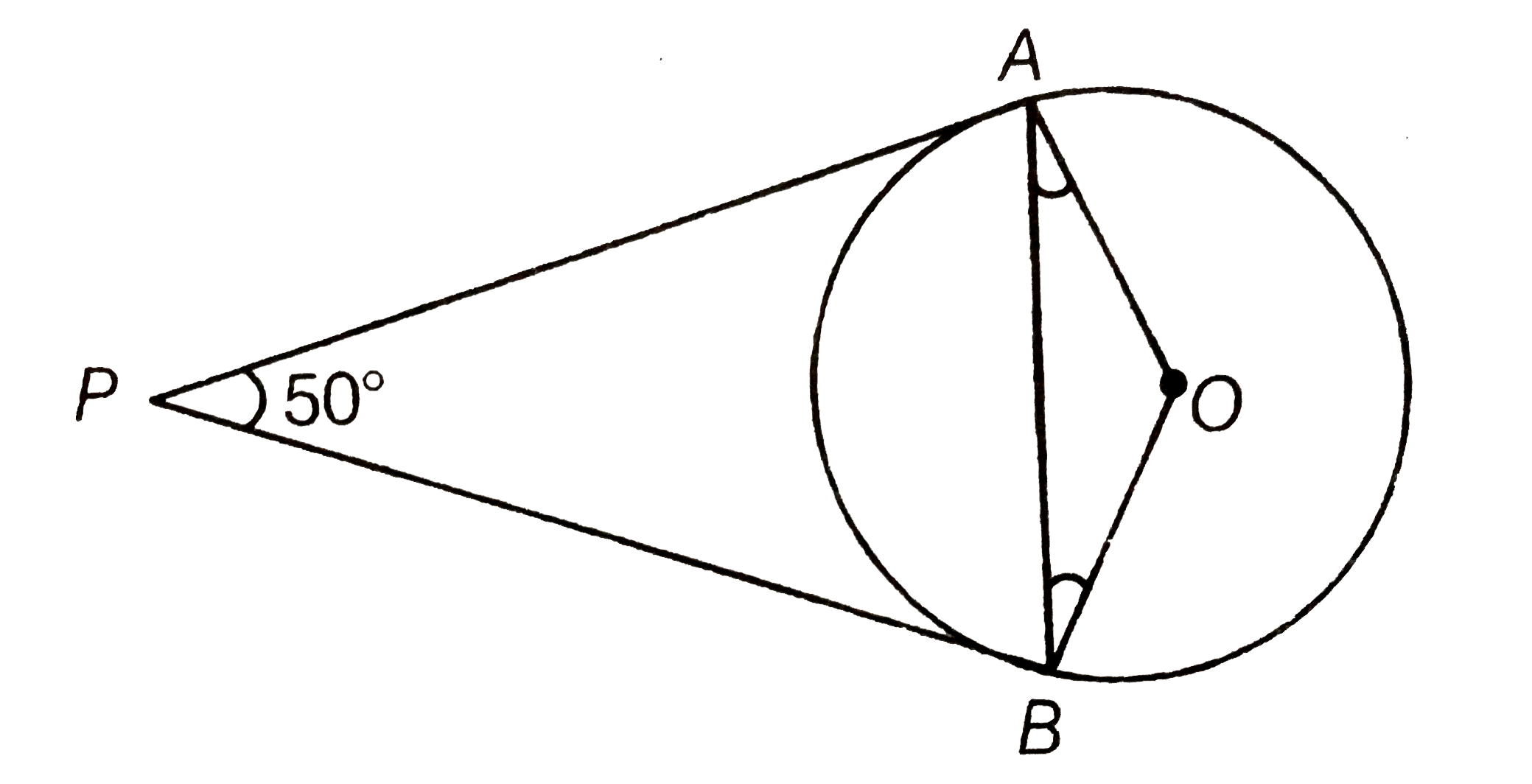 A25∘B30∘C40∘D50∘
A25∘B30∘C40∘D50∘
Two tangent segments PA and PB are drawn to a circle with centre O such that ∠APB=120o . Prove that OP=2 AP .
View SolutionIn the given figure PA and PB are tangents to a circle with centre O. if ∠APB=(2x+3)∘ and ∠AOB=(3x+7)∘. then find the value of x.
View SolutionAssertion (A) : PA and PB are triangles to a circle with centre O such that ∠AOB=110∘, then ∠APB=90∘
Reason (R ) : The length of two tangents drawn from an external point are equal .
View SolutionPA and PB are the tangent on a circle with centre O such that ∠APB=42∘. What will be the value of ∠AOB?
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=40∘, then ∠OABis equal to:
View Solution