O is the circumcentre of ΔABC, given ∠BAC=85∘and∠BCA=55∘, find ∠OAC.
40∘
50∘
60∘
80∘
The correct Answer is:B
To find the angle ∠OAC in triangle ΔABC where O is the circumcenter, we can follow these steps:
1. Identify Given Angles:
- We are given ∠BAC=85∘ and ∠BCA=55∘.
2. Calculate Angle ABC:
- We know that the sum of angles in a triangle is 180∘. Therefore, we can find ∠ABC using the formula:
∠ABC=180∘−∠BAC−∠BCA
- Substituting the known values:
∠ABC=180∘−85∘−55∘=40∘
3. Understanding the Circumcenter:
- The circumcenter O of triangle ABC is the point where the perpendicular bisectors of the sides intersect. It is also the center of the circumcircle of the triangle.
4. Identify Angles in Triangle PAC:
- In triangle PAC, we need to find ∠OAC. We know that the angle ∠APC is 90∘ because O lies on the perpendicular bisector.
5. Apply the Triangle Angle Sum Property:
- Using the triangle angle sum property in triangle PAC:
∠PAC+∠APC+∠ACB=180∘
- Substituting the known angles:
∠PAC+90∘+55∘=180∘
6. Solve for Angle PAC:
- Rearranging the equation gives:
∠PAC=180∘−90∘−55∘=35∘
7. Conclusion:
- Since ∠OAC is equal to ∠PAC, we find:
∠OAC=35∘
Final Answer:
∠OAC=35∘
- We are given ∠BAC=85∘ and ∠BCA=55∘.
- We know that the sum of angles in a triangle is 180∘. Therefore, we can find ∠ABC using the formula:
∠ABC=180∘−∠BAC−∠BCA
- Substituting the known values:
∠ABC=180∘−85∘−55∘=40∘
- The circumcenter O of triangle ABC is the point where the perpendicular bisectors of the sides intersect. It is also the center of the circumcircle of the triangle.
- In triangle PAC, we need to find ∠OAC. We know that the angle ∠APC is 90∘ because O lies on the perpendicular bisector.
- Using the triangle angle sum property in triangle PAC:
∠PAC+∠APC+∠ACB=180∘
- Substituting the known angles:
∠PAC+90∘+55∘=180∘
- Rearranging the equation gives:
∠PAC=180∘−90∘−55∘=35∘
- Since ∠OAC is equal to ∠PAC, we find:
∠OAC=35∘
∠OAC=35∘
Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF
25 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)
70 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
Knowledge Check
O is the circumcentre of ΔABC, given ∠BAC=85∘and∠BCA=55∘, find ∠OAC.
A40∘B50∘C60∘D80∘O is the circumcentre of the triangle ABC and ∠BAC=85∘, ∠BCA=75∘ , then the value of ∠OAC is
A55∘B150∘C20∘D70∘‘O' is the orthocentre of △ABC.Then ∠BOC+∠BAC is equal to:
O, △ABC में, △ABC का लंबकेंद्र है, तो ∠BOC+∠BAC कितना होगा?A120∘B135∘C180∘D90∘
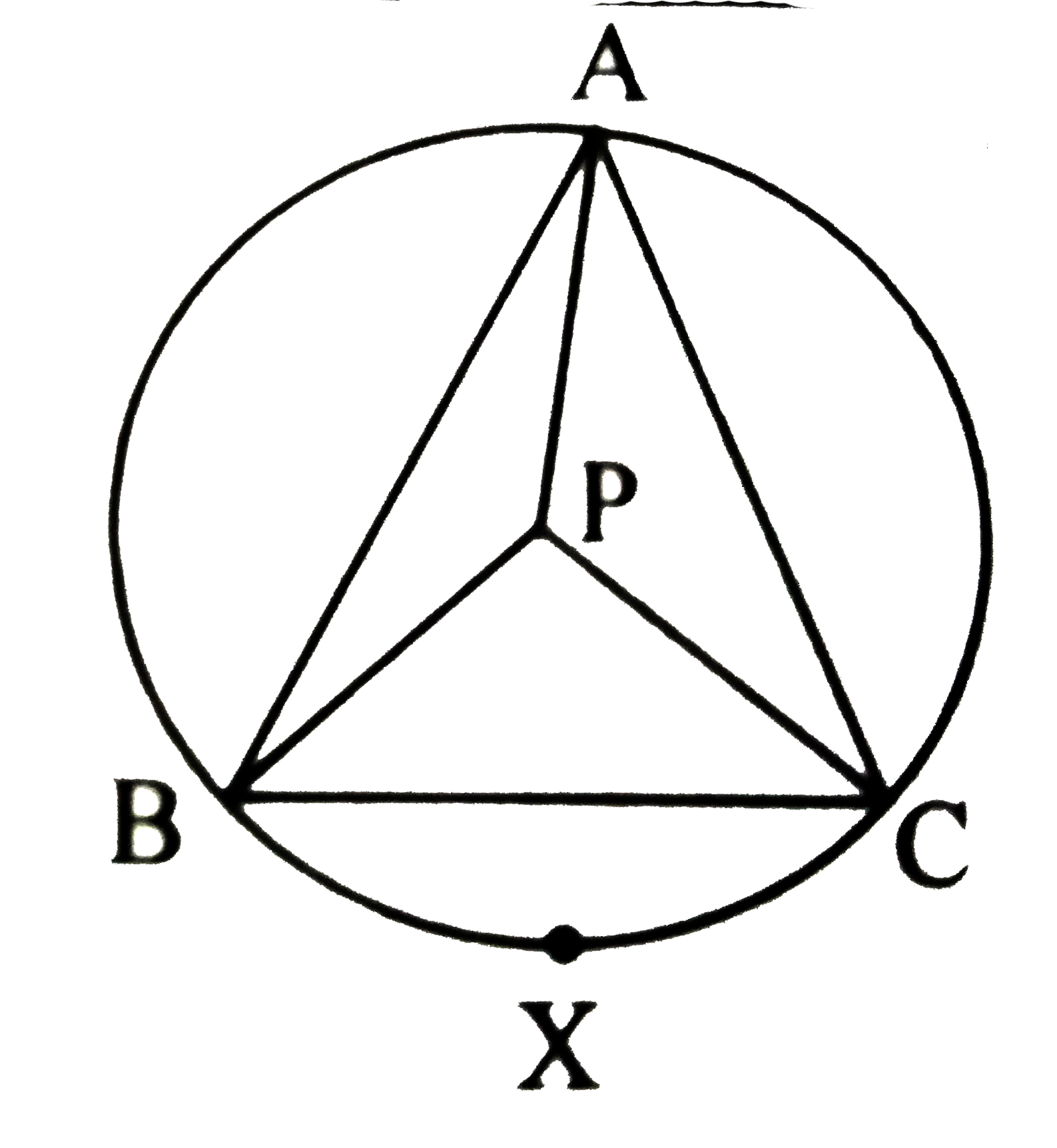
In the adjoining figure, P is the circumcentre of the ΔABC.m∠APC=118∘ and m∠PBC=45∘ , then find:
(i) m(arc BXC)
(ii) m(arc BCA)
View SolutionIn ΔABC,AC=BC and ∠BAC=70∘. Find ∠BCA
View SolutionIf O is a circumcentre of ΔABC and OD⊥BC the find ∠BOD?
View SolutionO is the circumcentre of a triangle ABC. If ∠BAC=85∘and∠BCA=75∘ then what is the value of ∠OAC?
View SolutionO is the circumcentre of the isosceles ΔABC. Given that AB = AC = 17 cm and BC = 6 cm. The radius of the circle is
View Solution
