ABCD is a square EF is parallel to BD. R is the mid-point of EF. Prove that :
(i) BE=DF
(ii) AR bisects angle BAD
(iii) If AR produced it will pass through C.

(i) only
(ii) only
Both (i) and (ii)
Neither (i) nor (ii)
The correct Answer is:C
Step by step video, text & image solution for ABCD is a square EF is parallel to BD. R is the mid-point of EF. Prove that : (i) BE = DF (ii) AR bisects angle BAD (iii) If AR produced it will pass through C. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Integer/Numerical Value Type)
10 Videos
- PROBABILITYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
In the figure, ABCD is a square and EF is parallel to BD. R is the mid-point of EF. Prove that (i) BE= DF (ii) AR bisects ∠BAD and (iii) If AR is produced it will pass through C.
View SolutionIn parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Provethat:(i) AE=AD(i) DE bisects ∠ADC and(ili) Angle DEC is a right angle.
View SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).

View SolutionABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that ar(△AXY)=38ar(∣∣gmABCD)
View SolutionAC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters (ii) ABCD is a rectangle
View SolutionIn parallelogram ABCD, X and Y are mid-points of opposite sides AB and DC respectively. Prove that: (i)AX=YC (ii) AX is parallel to YC (iii)AXCY is parallelogram
View SolutionACandBD are chords of a circle which bisect each other. Prove that (i) ACandBD are diameters (ii) ABCD is a rectangle.
View SolutionABCD is a quadrilateral in which AD = BC and ∠DAB=∠CBA Prove that (i) ΔABD≅ΔBAC (ii) BD = AC (iii) ∠ABD=∠BAC
View SolutionIn Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
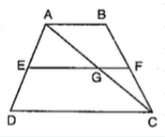
View SolutionIn the figure ABCD is a trapezium in which side AB is parallel to side DC and E is the midpoint of side AD. If F is a point on the side BC such that the line segment EF is parallel to DC.Prove that Fis the mid-point of BC and EF=12(AB+DC)
View Solution