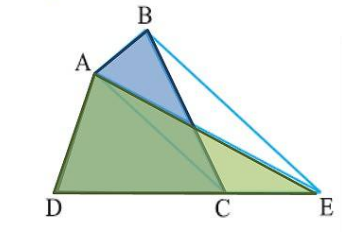
In Figure, ABCD is a quadrilateral and BE∣AC and also BE meets DC produced at E. Show that area of ADE is equal to the area of the quadrilateral ABCD
Step by step video & image solution for In Figure, A B C D is a quadrilateral and B E|A C and also B E meets D C produced at Edot Show that area of A D E is equal to the area of the quadrilateral A B C D by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - SOLVED EXAMPLES
14 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - NCERT SECTION ( EXERCISE 9.1)
1 Videos
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - OLYMPIAD/HOTS CORNER
6 Videos
Similar Questions
In Figure, ABCD is a quadrilateral and BE∣AC and also BE meets DC produced at E. Show that area of ADE is equal to the area of the quadrilateral ABCD
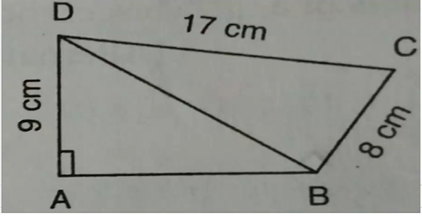
View SolutionIn the given figure, compute the area of quadilateral
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC−EDA.
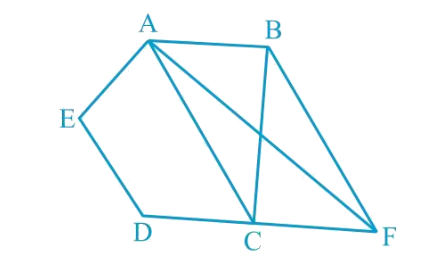
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that ar(ACB)=ar(ACF) (ii) ar(AEDF)=ar(ABCDE)
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that: ar (ACB)=ar (ACF) ar (AEDF)=ar (ABCDE)
View SolutionIf the diagonals AC,BD of a quadrilateral ABCD, intersect at O, and seqarate the quadrilateral into four triangles of equal area, show that quadrilateral ABCD is a parallelogram. GIVEN : A quadrilateral ABCD such that its diagonals AC and BD intersect at O and separate it into four parts such that ar(AOB)=ar(BOC)=ar(COD)=ar(AOD) TO PROVE : Quadrilateral ABCD is a parallelogram.
View SolutionE,F,G,H are respectively, the mid-points of the sides AB,BC,CD and DA of parallelogram ABCD . Show that the quadrilateral EFGH is a parallelogram and that its area is half the area of the parallelogram, ABCD. GIVEN : A quadrilateral ABCD in which L,F,G,H are respectively the mid-points of the sides AB,BC,CD and DA. TO PROVE : (i) Quadrilateral EFGH is a parallelogram ar(^(gm)EFGH)=12ar(^(gm)ABCD) CONSTRUCTION : Join AC and HF
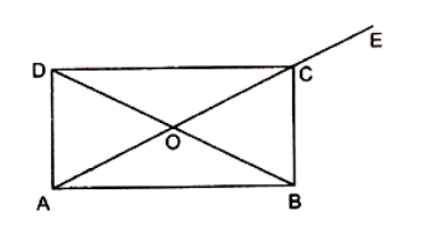
View SolutionIn Figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD=1460, find ∠AOB
View SolutionABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P as shown in Figure. Prove that ar (ABP)=ar (Qua..ABCD).
View SolutionProve that the diagonals of quadrilateral ABCD,AC and BD intersect in O. Prove that if BO=OD, the triangles ABC and ADC are equal in area.
View Solution
