ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=12ar(ΔABC).
Step by step video & image solution for ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar (DeltaBDE) = (1)/(2) ar (DeltaABC). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Multiple Choice Questions )
45 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE (Match the Following )
2 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - NCERT SECTION ( EXERCISE 9.3)
19 Videos
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - OLYMPIAD/HOTS CORNER
6 Videos
Similar Questions
ABC and BDE are two equilateral triangles such that D is the mid-point of BC . The ratio of the areas of the triangles ABC and BDE is 2:1 (b) 1:2 (c) 4:1 (d) 1:4
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
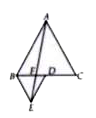
ar(ΔBDE) = 1/4 ar(ΔABC)
View Solution
Knowledge Check
ABC and BDE are two equilateral triangle such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
A2:1B1:2C4:1D1:4
In figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
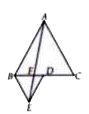
ar(ΔBDE) = 1/2 ar(ΔBAE)
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
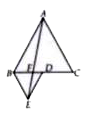
ar(ΔABC) = 2 ar(ΔBEC)
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
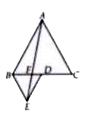
ar(ΔBFE) = 2 ar(ΔFED)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. If the area of triangle ABC is 136cm2, then the area of triangle BDE is equal to:
ABC और BDE दो समबाहु त्रिभुज हैं जेसे D, BC का मध्य-बिंदु है। यदि त्रिभुज ABC का क्षेत्रफल 136cm2, है, तो त्रिभुज BDE का क्षेत्रफल ज्ञात करे
View SolutionΔABCandΔCDE are two equilateral triangles such that D is the mid -point of BC . The ratio of the areas of ΔCDEandΔABC is 1 : k then k =
View SolutionIn the figure, ABC and BDE are two equilateral triangle such that D is the mid-point of BC. If AE intersects BC at F, show that:
(i) ar(ΔBDE)=14ar(ΔABC) (ii) ar(ΔBDE)=12ar(ΔBAE)
(iii) ar(ΔABC)=2ar(ΔBEC) (iv) ar(ΔBFE)=ar(ΔAFD)
(v) ar(ΔBFE)=2ar(ΔFED) (vi) ar(ΔFED)=18ar(ΔAFC)

View SolutionTick the correct answer and justify:ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(A) 2:1 (B) 1:2 (C) 4:1 (D) 1:4
View Solution
