Two triangles ABC and CDE are such that AC = EC, BC = DC, $∠ E = 60^{\circ} and ∠ D C E = 30^{\circ} and ∠ B = 90^{\circ}$ . Show that the triangles are congruent, (see the figure below).

Video Solution

Answer

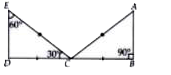
Step by step video & image solution for Two triangles ABC and CDE are such that AC = EC, BC = DC, angleE=60^(@)andangleDCE=30^(@)andangleB=90^(@). Show that the triangles are congruent, (see the figure below). by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.

Updated on:21/07/2023

Class 7 MATHS CONGRUENCE OF TRIANGLES

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
In two triangle ABC and DEF, AB= DE ,BC=DF and AC =Ef then
A $△ A B C ≅ △ D E F$
B $△ A B C ≅ △ F E D$
C $△ A B C ≅ △ E S E$
DNone of these
Question 2 - Select One
In two triangles ABC and FDE, $∠ B = ∠ D = 90^{\circ}$ , AC = FE and BC = DE. Then $∠ F$ = ____.
A $∠ C$
B $∠ A$
C $∠ B$
Dcan't be determined
Question 3 - Select One
ABC is a triangle, where BC = 2AB , $∠$ B = $30^{\circ}$ and $∠$ A = $90^{\circ}$ . The magnitude of the side AC is
A $\frac{2 B C}{3}$
B $\frac{3 B C}{4}$
C $\frac{B C}{\sqrt{3}}$
D $\frac{\sqrt{3} B C}{2}$

MTG IIT JEE FOUNDATION-CONGRUENCE OF TRIANGLES -Subjective Problems (Long Answer Type)

Home
Ask Doubt
Profile

Two triangles ABC and CDE are such that AC = EC, BC = DC, ∠E=60∘and∠DCE=30∘and∠B=90∘. Show that the triangles are congruent, (see the figure below).

Topper's Solved these Questions

Similar Questions

Knowledge Check

In two triangle ABC and DEF, AB= DE ,BC=DF and AC =Ef then

In two triangles ABC and FDE, ∠B=∠D=90∘, AC = FE and BC = DE. Then ∠F = ____.

ABC is a triangle, where BC = 2AB , ∠B = 30∘ and ∠A = 90∘. The magnitude of the side AC is

MTG IIT JEE FOUNDATION-CONGRUENCE OF TRIANGLES -Subjective Problems (Long Answer Type)

Two triangles ABC and CDE are such that AC = EC, BC = DC, $∠ E = 60^{\circ} and ∠ D C E = 30^{\circ} and ∠ B = 90^{\circ}$ . Show that the triangles are congruent, (see the figure below).

In two triangles ABC and FDE, $∠ B = ∠ D = 90^{\circ}$ , AC = FE and BC = DE. Then $∠ F$ = ____.

ABC is a triangle, where BC = 2AB , $∠$ B = $30^{\circ}$ and $∠$ A = $90^{\circ}$ . The magnitude of the side AC is