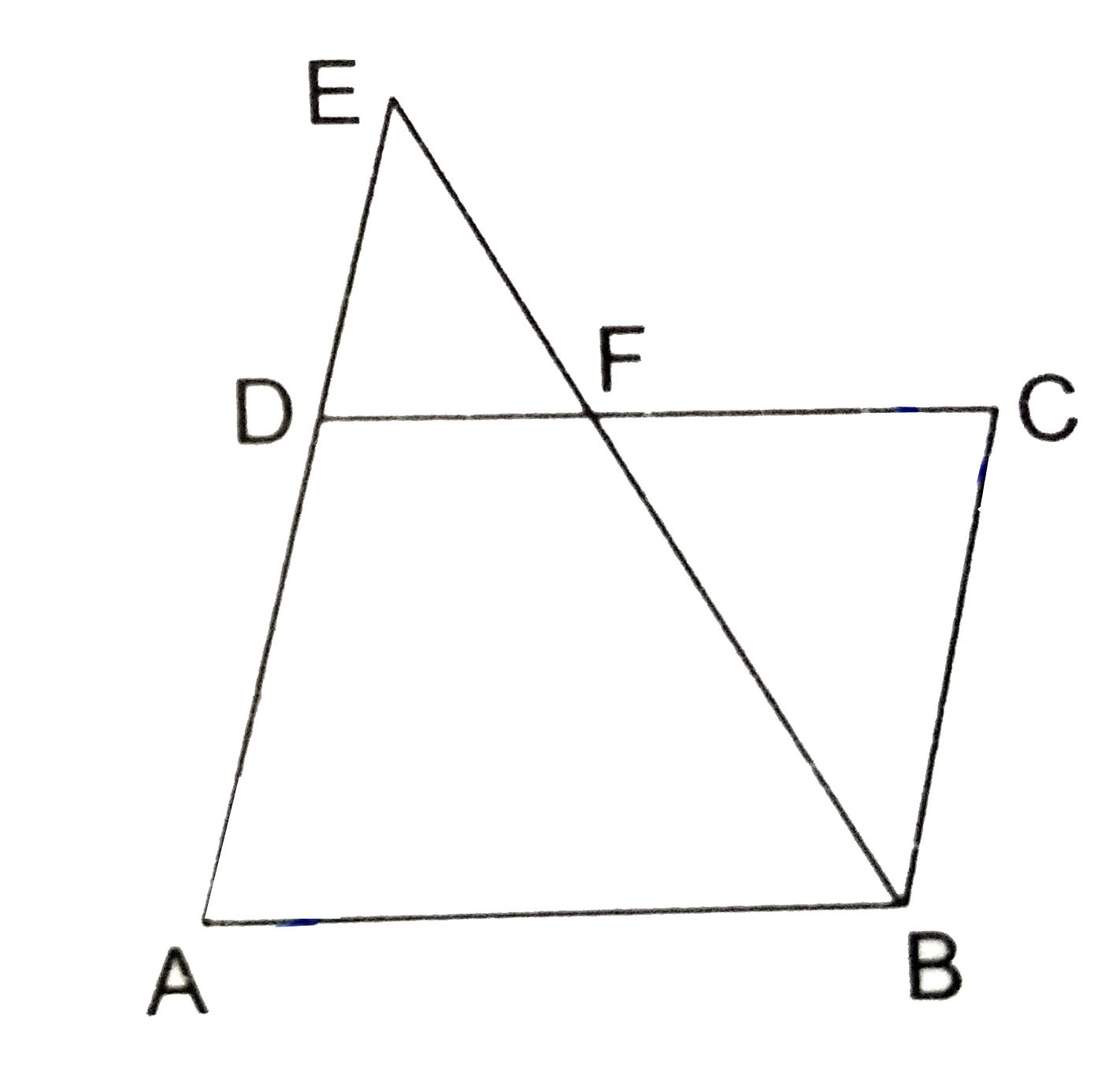
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F . Show that ΔABE~ΔCFB .
To prove that triangles ΔABE and ΔCFB are similar, we will use the properties of angles in a parallelogram and the concept of corresponding angles.
1. Identify the Parallelogram and Points:
- Let ABCD be a parallelogram where E is a point on the extended line of side AD.
- The line BE intersects CD at point F.
2. Use Properties of Parallelograms:
- In parallelogram ABCD, opposite angles are equal. Therefore, we have:
∠A=∠C
3. Identify Alternate Interior Angles:
- Since BE is a transversal line intersecting the parallel lines AD and BC, the alternate interior angles are equal. Thus, we have:
∠EBA=∠CBF
4. Establish Corresponding Angles:
- We have established that:
- ∠A=∠C (from the properties of the parallelogram)
- ∠EBA=∠CBF (from the alternate interior angles)
5. Apply the Angle-Angle (AA) Criterion for Similarity:
- Since we have two pairs of angles that are equal, we can conclude that:
ΔABE∼ΔCFB
- This is based on the AA criterion for triangle similarity, which states that if two angles of one triangle are equal to two angles of another triangle, then the triangles are similar.
Conclusion:
Thus, we have shown that ΔABE is similar to ΔCFB.
- Let ABCD be a parallelogram where E is a point on the extended line of side AD.
- The line BE intersects CD at point F.
- In parallelogram ABCD, opposite angles are equal. Therefore, we have:
∠A=∠C
- Since BE is a transversal line intersecting the parallel lines AD and BC, the alternate interior angles are equal. Thus, we have:
∠EBA=∠CBF
- We have established that:
- ∠A=∠C (from the properties of the parallelogram)
- ∠EBA=∠CBF (from the alternate interior angles)
- Since we have two pairs of angles that are equal, we can conclude that:
ΔABE∼ΔCFB
- This is based on the AA criterion for triangle similarity, which states that if two angles of one triangle are equal to two angles of another triangle, then the triangles are similar.
Thus, we have shown that ΔABE is similar to ΔCFB.
Topper's Solved these Questions
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6.4
9 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6.5
21 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6.2
12 Videos
- SURFACE AREAS AND VOLUMESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
Similar Questions
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE~ΔCFB.
View SolutionIf E is a point on side AD produced of a parallelogram ABCD and BE intersects CD at F . Prove that DABE~DCFB .
View SolutionE si a point on side AD produced of a parallelogram ABCD and BE intersects DC at F. prove that △ABE~△CFB.
View SolutionThe side AD of parallelogram ABCD is produced to a point E. BE intersects CD at F. Show that ΔABE~ΔCFB.
View SolutionA point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar(ΔADF)=ar(ABFC).
View SolutionP and Q are the mid-point of the oposite sides AB and CD of a parallelogram ABCD. AQ interects DP at S and BQ interects CP at R. Show that PQRS is a parallelogram.

View SolutionThrough the mid-point M of the side CD of a parallelogram ABCD , the line BM is drawn intersecting AC at LandAD produced at E . Prove that EL=2BL.
View SolutionABCD is a trapezium with AB || DC. E is midpoint of side AD. From point E a line is drawn parallel to AB that intersects BC at F. Show that F is midpoint of BC.
View SolutionIn quadrilateral ABCD, AB||CD and BC||AD. Show that
(i) ΔABD≅ΔCDB

View SolutionABCD is a parallelogram. The circle through A,B and intersects CD produced at E. show that AD =AE.
View Solution
