In Figure 2, Delta ABD is a right triangle, right-angled at A and AC _|_ BD. Prove that AB* = BC . BD.
The correct Answer is:=BC×BD
Step by step video, text & image solution for In Figure 2, Delta ABD is a right triangle, right-angled at A and AC _|_ BD. Prove that AB* = BC . BD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6 .612videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Multiple Choice Questions) (LEVEL -1 )35videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6.49videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER20videos
SURFACE AREAS AND VOLUMES
Similar Questions
ΔABD is a right triangle, right-angled at A and AC⊥BD. Prove that AB2=BC×BD.
View SolutionABC is a right triangle right angled at C and AC = √3BC . Prove that ∠ABC=60∘ .
View SolutionABC is a right triangle right-angled at CandAC=√3BC . Prove that ∠ABC=600.
View SolutionIn the figure given below ABC is a triangle right angled at A and AC ⊥ BD . Show that
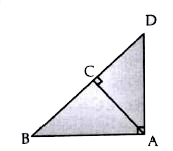
AB2=BC×BDView SolutionIn the figure , ABD is a triangle right angled at A and AC ⊥ Bd . Show that
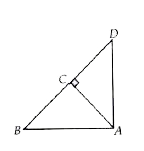
AD2=BD⋅CDView SolutionIn the figure given below ABC is a triangle right angled at A and AC ⊥ BD . Show that
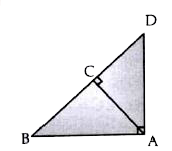
AD2=BD×DCView SolutionABC is an isosceles right triangle right-angled at C . Prove that AB2=2AC2 .
View SolutionABC is an isosceles right triangle, right-angled at C . Prove that: AB2=2AC2.
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
View SolutionIn the given figure, ΔABC is an obtuse triangle, obtuse-angled at B. If AD⊥CB (produced ) prot that AC2=AB2+BC2+2BC⋅BD
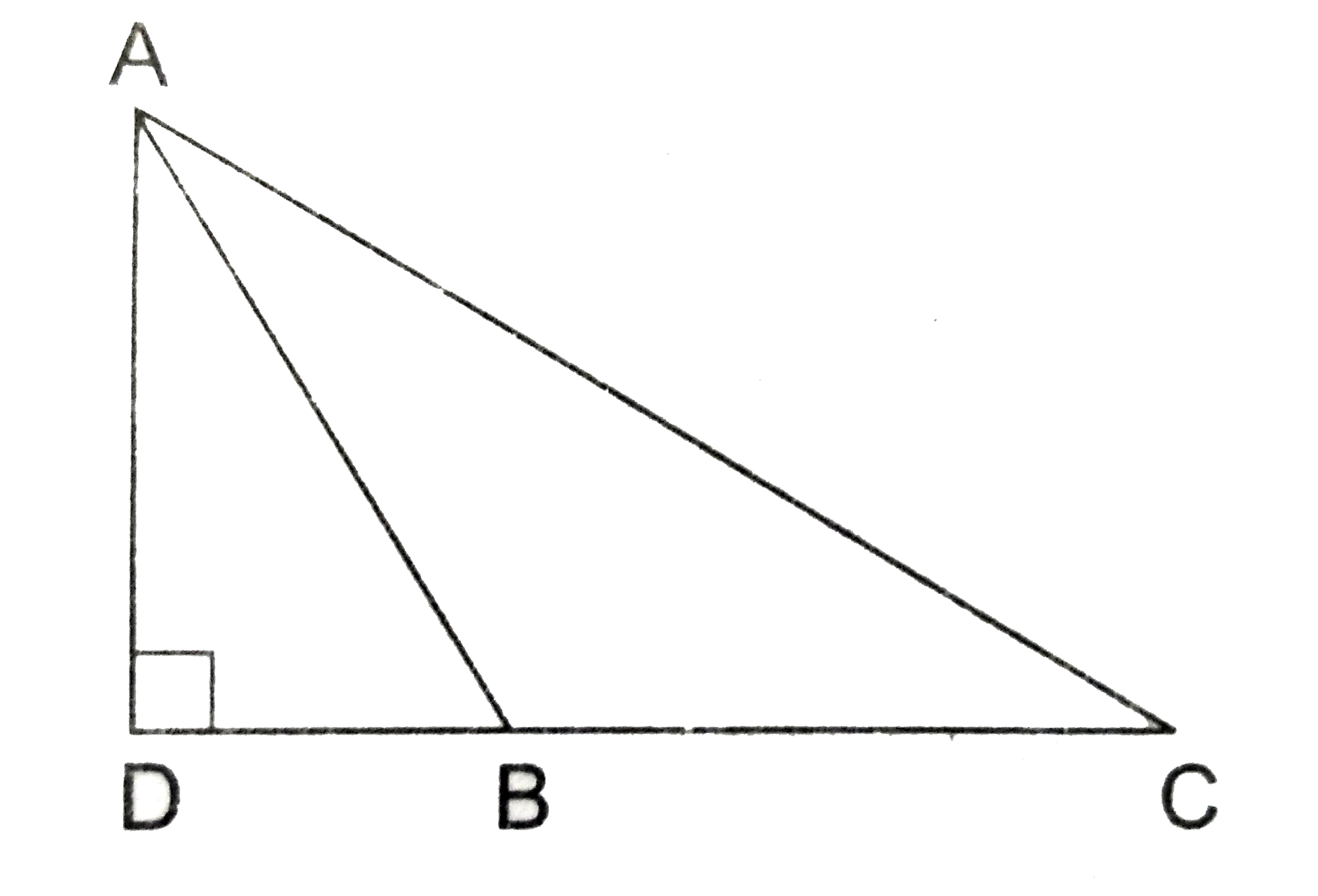 View Solution
View Solution

