Derive electric field intensity due to uniformity charged infinite plane sheet

Text Solution

Verified by Experts

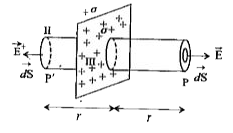
Consider a thin infinite plane sheet.
Let P = be a point where we want to find electric field intensity $\to E$ .
$σ =$ be the surface charge density.
$i . e ., σ = \frac{q}{A}$ $∴$ the charge enclosed by Gaussian surface,
$q = σ A$
According to Gauss is theorem
$\oint S \to E . - \to d S = \frac{q}{ɛ_{0}} = \frac{σ A}{ɛ_{0}}$
Gaussian surface is divided into three parts I, II and III.
$∴$ From (1)
$\oint I \to E . - \to d S + \oint I I \to E . - \to d S + \oint I I I \to E . - \to d S = \frac{σ A}{ɛ_{0}} ... (2)$
$\oint I E p S cos θ + \oint I I E p S cos θ + \oint I I I E p S cos θ = \frac{σ A}{ɛ_{0}}$
$\oint I E p S {cos 0}^{\circ} + \oint I I E p S {cos 0}^{\circ} + \oint I I I E p S {cos 90}^{\circ} = \frac{σ A}{ɛ_{0}}$
$\oint I E p S + \oint I I E p S + 0 = \frac{σ A}{ɛ_{0}}$
$\oint I E p S (1) + \oint I I E p S (1) = \frac{σ A}{ɛ_{0}}$
$\oint I E p S + \oint I I E p S = \frac{σ A}{ɛ_{0}}$
Since electric field intensity E is constant at every point of Gaussian surface,
$∴ E \oint I d s + E \oint I I d s = \frac{σ A}{ɛ_{0}}$
$E A + E A = \frac{σ A}{ɛ_{0}}$
$2 E A = \frac{σ A}{ɛ_{0}}$
$E A = \frac{σ A}{2 ɛ_{0}}$
$∴ E = \frac{σ A}{2 ɛ_{0} A}$
$∴ E = \frac{σ}{2 ɛ_{0}}$
$∴$ In vector from
$\to E = \frac{σ}{2 ɛ_{0}} ˆ n$ , where $ˆ n$ is a unit vector perpendiculars to the plane of sheet.
The electric field is directed away from the sheet if it is positively, charged and it is directed towards the sheet if it is negatively charged.
Special Case
If the plane sheet has a finite thickness, then charges on both sides of sheet are to be considered.
$∴ E = \frac{2 σ A}{2 ɛ_{0} A}$
$∴ E = \frac{σ}{ɛ_{0}}$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Similar Questions

Knowledge Check

The expression for electric field intensity at a points outside uniformly charged thin plane sheet is (where, d is the distance of point from plane sheet)
Aindependent of d
Bdirectly proportional to $\sqrt{d}$
Cdirectly proportional to d
Ddirectly proportional to $\frac{1}{\sqrt{d}}$

Recommended Questions

Home
Ask Doubt
Profile