With the help of a neat diagram derive the expression for the effective resistance when three resistors $R_{1}, R_{2} and R_{3}$ are connected is series.

Text Solution

Verified by Experts

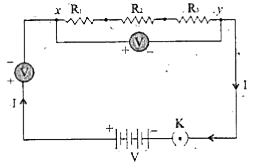
Let the potential difference across the resistors $R_{1}, R_{2} and R_{3}$ are, $V_{1}, V_{2} and V_{3}$ respectively. In the electric circuit shown above, let I be the current through the circuit. In this case, the current through each resistor is also I and the potential difference across a combination of resistors is equal to the sum of potential differences across this individual resistors. That is
$V = V_{1} + V_{2} + V_{3} ... . (1)$
If the resistors $R_{1}, R_{2}$ and $R_{3}$ are replaced by an equivalent single resistor R, such that the potential difference V across it, and current I through the circuit remain the same, then, applying the Ohm.s law to the entire circuit and three. resistors separately, we have
$V = I R ... (2)$
$V_{1} = I R_{1} ... . (3)$
$V_{2} = I R_{2}$
$V_{3} = I R_{3} ... . . (4)$
By adding (3), (4) and (5), we get
$V_{1} + V_{2} + V_{3} = I R_{1} + I R_{2} + I R_{3}$
or $V_{1} + V_{2} + V_{3} (R_{1} + R_{2} + R_{3})$ .
By using equation (1)
$V = I (R_{1} + R_{2} + R_{3})$
By using equation (2)
$I R = I (R_{1} + R_{2} + R_{3})$ .
or $R = R_{1} + R_{1} + R_{3}$

Updated on:21/07/2023