Question

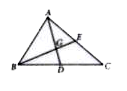
In triangle ABC, AD, BE and CF are the medians intersecting at point G and area of triangle ABC is $156c{m}^2$. What is the area (in $c{m}^2$) of triangle FGE ?

Options

A. 13
B. 26
C. 39
D. 52

Answer

A

Explanation

To find the area of triangle FGE in triangle ABC, where AD, BE, and CF are the medians intersecting at point G, and the area of triangle ABC is given as 156 cm², we can follow these steps:

1. Understanding the Medians and Centroid:
- In triangle ABC, the medians AD, BE, and CF intersect at point G, which is the centroid of the triangle. The centroid divides each median into two segments, with the segment connecting the vertex to the centroid being twice the length of the segment connecting the centroid to the midpoint of the opposite side.

2. Area of Triangle DEF:
- The area of triangle DEF, formed by the midpoints of the sides of triangle ABC, is known to be one-fourth of the area of triangle ABC.
- Therefore, we calculate the area of triangle DEF:
\( \text{Area of triangle DEF} = \frac{1}{4} \times \text{Area of triangle ABC} = \frac{1}{4} \times 156 \, \text{cm}^2 = 39 \, \text{cm}^2 \)

3. Area of Triangle FGE:
- Triangle FGE is formed by the segments connecting the centroid G to the midpoints of sides AB and AC (points E and F).
- The area of triangle FGE can be found by recognizing that triangle FGE is one-third of the area of triangle DEF. This is because the centroid divides the area of triangle DEF into three smaller triangles (DGF, DGE, and FGE) of equal area.
- Therefore, we calculate the area of triangle FGE:
\( \text{Area of triangle FGE} = \frac{1}{3} \times \text{Area of triangle DEF} = \frac{1}{3} \times 39 \, \text{cm}^2 = 13 \, \text{cm}^2 \)

4. Final Answer:
- The area of triangle FGE is \( 13 \, \text{cm}^2 \).

Summary:
The area of triangle FGE is \( 13 \, \text{cm}^2 \).