In a triangle ABC, ∠ABC=90∘,∠ACB=30∘,AB=5cm. What is the length of AC?
10 cm
5 cm
5√2 cm
5√3cm
To find the length of AC in triangle ABC, where angle ABC = 90°, angle ACB = 30°, and AB = 5 cm, we can use the properties of right triangles and trigonometric ratios.
1. Identify the Triangle and Angles:
- We have triangle ABC with:
- Angle ABC = 90° (right angle)
- Angle ACB = 30°
- Therefore, angle CAB = 60° (since the sum of angles in a triangle is 180°).
2. Use the Sine Function:
- In a right triangle, the sine of an angle is defined as the ratio of the length of the opposite side to the length of the hypotenuse.
- Here, we will use the sine function for angle ACB (30°):
sin(30°)=Opposite side (AB)Hypotenuse (AC)
3. Substituting Known Values:
- We know that:
- sin(30°)=12
- AB = 5 cm (the side opposite to angle ACB)
- Plugging in the values, we have:
12=5AC
4. Cross-Multiplying to Solve for AC:
- Cross-multiply to find AC:
1⋅AC=2⋅5
AC=10 cm
5. Conclusion:
- The length of AC is 10 cm.
Final Answer:
AC = 10 cm
- We have triangle ABC with:
- Angle ABC = 90° (right angle)
- Angle ACB = 30°
- Therefore, angle CAB = 60° (since the sum of angles in a triangle is 180°).
- In a right triangle, the sine of an angle is defined as the ratio of the length of the opposite side to the length of the hypotenuse.
- Here, we will use the sine function for angle ACB (30°):
sin(30°)=Opposite side (AB)Hypotenuse (AC)
- We know that:
- sin(30°)=12
- AB = 5 cm (the side opposite to angle ACB)
- Plugging in the values, we have:
12=5AC
- Cross-multiply to find AC:
1⋅AC=2⋅5
AC=10 cm
- The length of AC is 10 cm.
AC = 10 cm
Similar Questions
In a right angled triangle ABCABC=90∘,ACB=30∘ and AB=8cm. Find the length of the other sides of the triangle.
View SolutionIf △ABC is a right angled triangle with ∠ABC=90∘, and AC = 10 cm and BC = 8 cm, then the length of AB is:
यदि △ABC एक समकोण त्रिभुज है, ∠ABC=90∘,AC =10, BC =8 cm फिर AB की लंबाई है:View Solution
Knowledge Check
- Question 1 - Select One
If ΔABC is right angled at B, AB = 30 and ∠ACB=60∘, then what is the value of AC?
A20B20√3C40D60 - Question 2 - Select One
In a right -angled triangle ABC, ∠ABC=90∘,AB=5cm and BC = 12 cm . The radius of t he circumcircle of the triangle ABC is
A7.5 cmB6 cmC6.5 cmD7cm
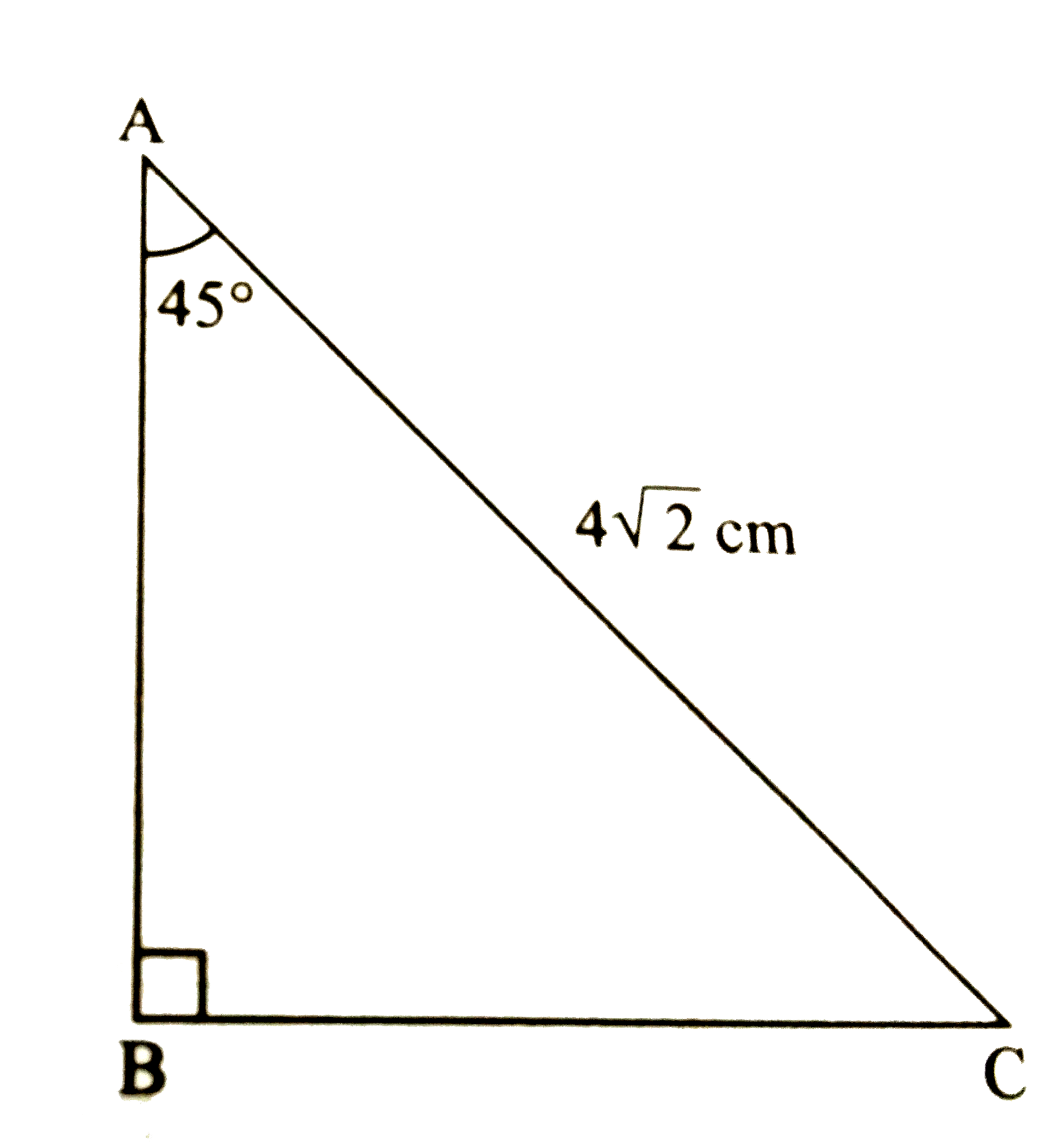
In △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
 View Solution
View SolutionIn a right-angled triangle ABC, if angle B=90°, BC = 3 cm and AC = 5 cm, then the length of side AB is
View SolutionABC is rt angled triangle ∠BAC=90∘and∠ACB=60∘. What is the ratio of the circum radius of the triagle to the side AB?
View SolutionABC is a triangle where BC = 2AB, ∠C=30∘ and ∠A=90∘. The magnitude of the side AC is:
View SolutionIn a triangle △ABC = AB = 13 cm, B C = 84 cm, and ∠AB=90∘, then length of AC will be
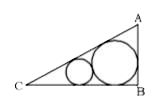
View SolutionIn the given figure, ABC is a right angled triangle. ∠ABC=90∘and∠ACB=60∘. If the radius of the smaller circle is 2 cm, then what is the radius (in cm) of the larger circle?
 View Solution
View Solution

