O is the any point on diagonal PR of parallelogram PQRS. Prove that Ar(PSO) = Ar(PQO)
∠PXSand∠QYR
∠XPS=∠QRY
PS=QR
∠PXS=∠QYR
∠PXS≅∠QYR
SO, XS=QY
area(POS)=1/2*B*H=1/2*PO*XS
area(POQ)=1/2*PO*QY
We proved XS and QY are same
Area of both the triangles are same.
Similar Questions
O is any point on the diagonal PR of a parallelogram PQRS (figure). Prove that ar(ΔPSO)=ar(ΔPQO).

View SolutionO is any point on the diagonal PR of a parallelogram PQRS (figure). Prove that ar(ΔPSO)=ar(ΔPQO).

View SolutionP is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△APD) = ar(△CPD).
View SolutionIn the adjacent figure P is a point inside the parallelogram ABCD. Prove that
ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
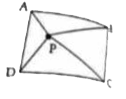
View SolutionIn the adjacent figure P is a point inside the parallelogram ABCD. Prove that
ar (APB) + ar (PCD) = 12 ar (ABCD)
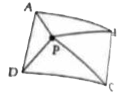
View SolutionIn Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that(i) ar(APB)+ar(PCD)=12ar(ABCD)(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
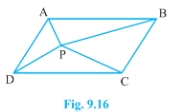
View SolutionIn the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(△APB)+ar(△PCD=12ar(ABCD)
(ii) ar(△APD)+ar(△PBC)=ar(△APB)+ar(△PCD)

View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
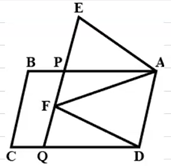
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).

View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogramABCD. Show that ar (APB) = ar (BQC).
View Solution
