In the given figure PQ,QRandRP touches a given circle respectively at point I,MandN. If ∠LMN=55∘and∠MNL=50∘, then find ∠P,∠Qand∠R
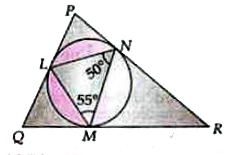
The correct Answer is:30∘
Step by step video, text & image solution for In the given figure PQ, QR and RP touches a given circle respectively at point I, M and N. If angle LMN = 55^(@) and angle MNL = 50^(@), then find angle P , angle Q and angle R by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8A71videos
CIRCLE AND ITS TANGENT LINES
- BOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B27videos
CIRCLE AND ITS TANGENT LINES
- BOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B8videos
CENTRE OF TRIANGLE
- BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B8videos
CONGRUENCE AND SIMILAR TRIANGLES
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, ∠A=60∘and∠ABC=80∘, then find ∠BPC.
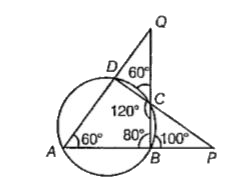 A40∘B45∘C20∘D30∘
A40∘B45∘C20∘D30∘ - Question 2 - Select One
In the given figure, O is the centre of the circle . AC and AB are the tangents to the circular at points P and Q , respectively. Also ∠RPC=55∘and∠RQB=60∘ then ∠PRQand∠QAP are, respectively .
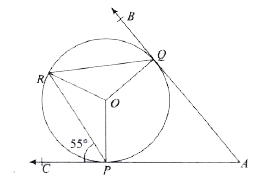 A50∘B60∘C30∘D40∘
A50∘B60∘C30∘D40∘ - Question 3 - Select One
In the figure , PQ and PR are tangent to the circle with centre O. Also, S is a point on the circle such that ∠SQC=50∘and∠SRM=60∘, then ∠QSR=
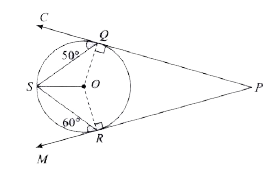 A40∘B70∘C80∘D45∘
A40∘B70∘C80∘D45∘
In the given, figure , O is the centre of the circle and AD is a tangent to the circle at.A if ∠CAD=55∘ and ∠ADC=25∘, then find ∠ABO.
 View Solution
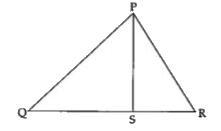
View SolutionIn ΔPQR it is given that = PQPR=QSSR. If ∠Q=70∘and∠R=50∘ then ∠QPS = ?
 View Solution
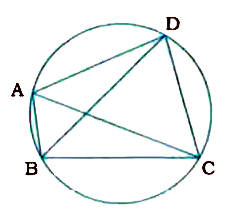
View SolutionIn the given figure ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC=55∘and∠BAC=45∘, find ∠BCD.
 View Solution
View Solution
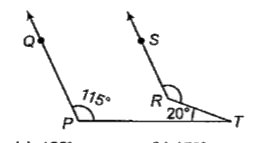
In the figure, PQ=QR,∠RPQ=60∘,and∠QRS=20∘. Find the measure of ∠QSR.View SolutionIn the given figure, if PQ∣∣RS,∠QPT=115∘and∠PTR=20∘, then ∠SRT is
 View Solution
View Solution

