In a triangle ABC, ∠ABC=90∘,∠ACB=30∘,AB=5cm. What is the length of AC?
10 cm
5 cm
5√2 cm
5√3 cm
The correct Answer is:A
Step by step video, text & image solution for In a triangle ABC, angleABC = 90^(@), angleACB = 30^(@), AB= 5 cm. What is the length of AC? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - TRIGONOMETRIC RATIO OF SPECIFIC ANGLESEXERCISE - Exercise 10B10videos
TRIGONOMETRIC RATIO OF SPECIFIC ANGLES
- BOOK - LUCENT PUBLICATIONCHAPTER - TRIGONOMETRIC RATIO OF SPECIFIC ANGLESEXERCISE - Exercise 10B10videos
TRIGONOMETRIC RATIO OF SPECIFIC ANGLES
- BOOK - LUCENT PUBLICATIONCHAPTER - QUADRILATERAL EXERCISE - Exercise 7B6videos
QUADRILATERAL
Similar Questions
In a right angled triangle ABCABC=90∘,ACB=30∘ and AB=8cm. Find the length of the other sides of the triangle.
View SolutionIf △ABC is a right angled triangle with ∠ABC=90∘, and AC = 10 cm and BC = 8 cm, then the length of AB is:
यदि △ABC एक समकोण त्रिभुज है, ∠ABC=90∘,AC =10, BC =8 cm फिर AB की लंबाई है:View Solution
Knowledge Check
- Question 1 - Select One
If ΔABC is right angled at B, AB = 30 and ∠ACB=60∘, then what is the value of AC?
A20B20√3C40D60 - Question 2 - Select One
In a right -angled triangle ABC, ∠ABC=90∘,AB=5cm and BC = 12 cm . The radius of t he circumcircle of the triangle ABC is
A7.5 cmB6 cmC6.5 cmD7cm
In △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
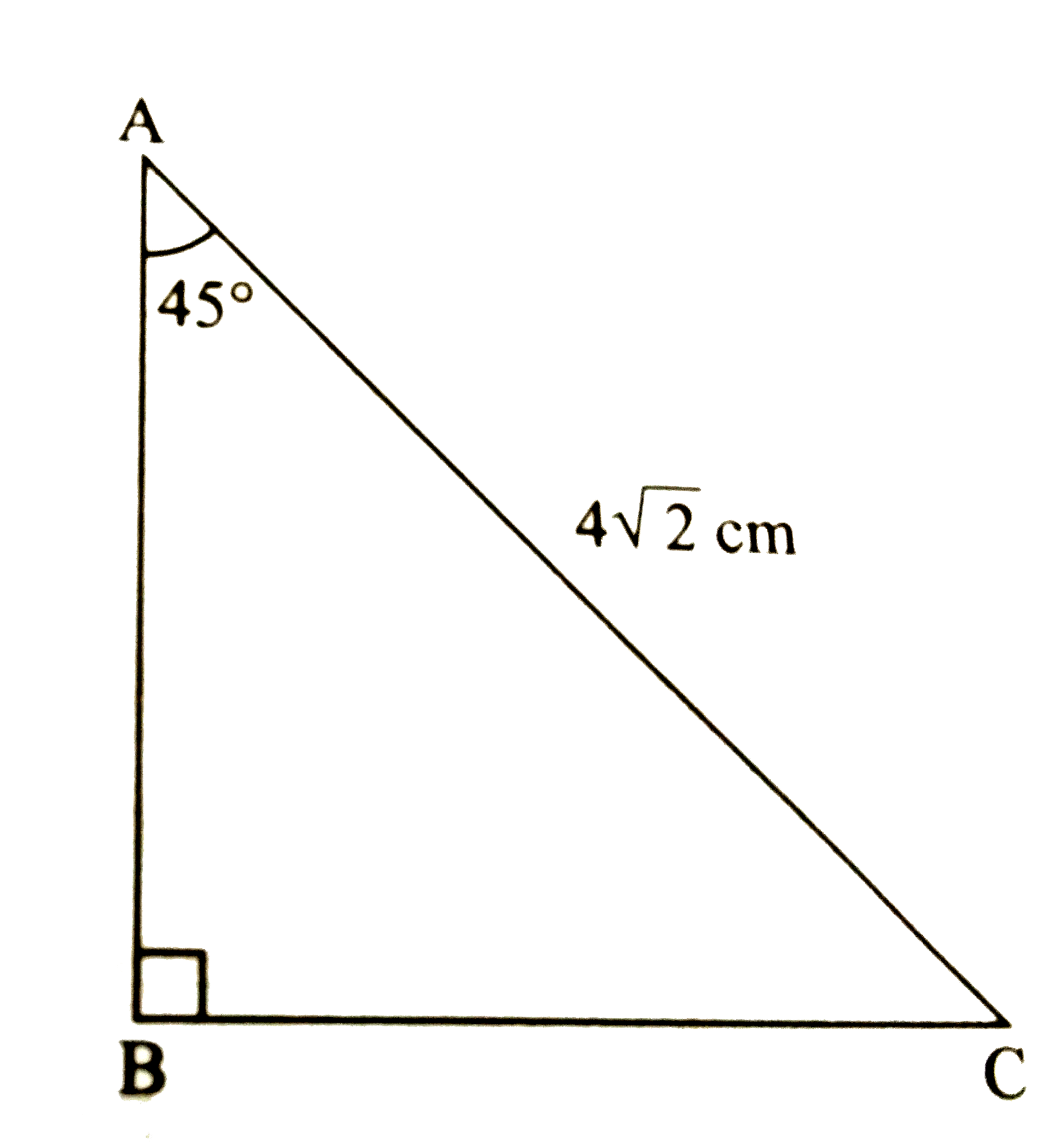 View Solution
View SolutionIn a right-angled triangle ABC, if angle B=90°, BC = 3 cm and AC = 5 cm, then the length of side AB is
View SolutionABC is rt angled triangle ∠BAC=90∘and∠ACB=60∘. What is the ratio of the circum radius of the triagle to the side AB?
View SolutionABC is a triangle where BC = 2AB, ∠C=30∘ and ∠A=90∘. The magnitude of the side AC is:
View SolutionIn a triangle △ABC = AB = 13 cm, B C = 84 cm, and ∠AB=90∘, then length of AC will be
View SolutionIn the given figure, ABC is a right angled triangle. ∠ABC=90∘and∠ACB=60∘. If the radius of the smaller circle is 2 cm, then what is the radius (in cm) of the larger circle?
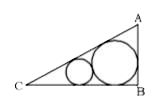 View Solution
View Solution

