கீழ்க்கண்ட “தவளையின் இதயம் வயிற்றுப்புறத் தோற்றம்” படத்தினில் குறிக்கப்பட்டுள்ள A, B, C மற்றும் D பாகங்களுக்கு சரியான விடையை தேர்ந்தெடு.
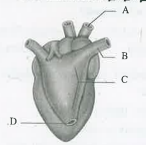
(அ) சைனஸ் வினோசஸ் - சிஸ்டமிக்தமனி - வலது பெருந்தமனி - மேற் பெருஞ்சிரை
(ஆ) மேற் பெருஞ்சிரை - சைனஸ் வினோசஸ் - சிஸ்டமிக்தமனி - வலது பெருந்தமனி
(இ) வலது பெருந்தமனி - மேற் பெருஞ்சிரை- சைனஸ் வினோசஸ் - சிஸ்டமிக்தமனி
(ஈ) சிஸ்டமிக்தமனி - மேற் பெருஞ்சிரை- சைனஸ் வினோசஸ் -கீழ் பெருஞ்சிரை
Topper's Solved these Questions
Similar Questions
முதன்மை வகைக்காட்டு காணப்படாதபோது அசலற்ற தொகுப்பிலிருந்து பெறப்பட்ட மாதிரி பெயர்ச்சொல் இவ்வாறு அறியப்படுகிறது.
View Solutionகீழ்க்கண்டவற்றுள் “தொகுதி நிடேரியா” பொருத்தவரையில் தவறான கூற்றைக் கண்டறி.
View SolutionIf a,b,candd are in H.P., then prove that (b+c+d)/a,(c+d+a)/b,(d+a+b)/c and (a+b+c)/d , are in A.P.
View SolutionIf A=[abcd] , then adj A is [−d−b−ca] (b) [d−b−ca] (c) [dbca] (d) [dcba]
View SolutionIf A={a,b},B={c,d},C={d,e} then {(a,c),(a,d)(a,e),(b,c),(b,d),(b,e)}=
View SolutionIf (a+b+c+d):(a+b−c−d)=(a−b+c−d):(a−b−c+d), then prove that a:b=c:d.
View SolutionIf (a+b+c+d)(a−b−c+d)=(a+b−c−d)(a−b+c−d), then prove that a:b=c:d
View SolutionIf a, b, c and d are four coplanr points, then prove that [abc]=[bcd]+[abd]+[cad].
View SolutionI : If a,b,c,d are four vectors then [b c d] a + [c a d] b + [a b c] c = [a b c]d
II : The points with position vectors a,b,c,d are coplanar then
[a b d] + [b c d] + [c a d] = [a b c]
View Solutionसत्य /असत्य
यदि A = {a, b, c, d) तथा फलन f ={(a,b), (b,d),(c,a),(d,c)} , तब f−1 = {(b,a),(d,b),(a,c),(c,d) } है।
View SolutionIf A={a,b},B={c,d},C={d,e}, then : {(a,c),(a,d),(a,e),(b,c),(b,d),(b,e)} is :
View Solutionபின்வரும் கணங்களின் ஆதி எண்ணைக் காண்க?R={x:x ஆனது முழுக்கள்,x∈Z மற்றும் -5≤x<5}
View Solutionபின்வரும் வகையீடுகளைப் பொருத்துக
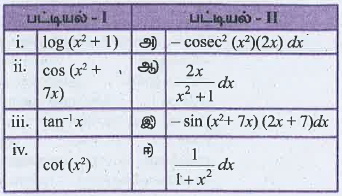 . சரியான பொருத்தமானது
. சரியான பொருத்தமானது
View Solutionm1மற்றும்m_2 என்ற இரண்டு நிறைகள் சமவிசையை உணர்கின்றன எனில், அவற்றின் முடுக்கங்களின் விகிதம்
View SolutionIf four sides of a quadrilateral ABCD are tangential to a circle, then AC+AD=BD+CD (b) AB+CD=BC+AD (c) AB+CD=AC+BC (d) AC+AD=BC+DB
View SolutionIn Figure, AD=BC and BD=CA. Prove that ∠A D B= ∠B C A a n d ∠D A B=∠ C B A.
View Solution
