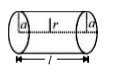
A solid cylindrical wire of length l has cross-section radius a as shown below. The specific resistance of material is given as $ρ = ρ_{0} r$ , where r is distance from axis of cylinder and $ρ_{0}$ is a positive constant quantity. The resistance across its ends is :

A

$\frac{ρ_{0} l}{2 π a}$

B

$\frac{ρ_{0} l}{π a^{2}}$

C

$\frac{ρ_{0} l}{π a}$

D

$\frac{2 ρ_{0} l}{π}$

Text Solution

Verified by Experts

The correct Answer is:A

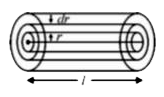
dR = Resistance of thin cylindrical shell of radius r and thickness (dr) $∴ d R = \frac{ρ l}{2 π r d r}$
Infinite number of thin cylinders are connected parallel to each other
$∴ \frac{1}{R} = \int \frac{1}{d R}$
$\Rightarrow \frac{1}{R} = \int \frac{2 π r d r}{ρ l} = \frac{2 π}{ρ_{0} l} a \int 0 \frac{r d r}{r}$
$\Rightarrow \frac{1}{R} = \frac{2 π a}{ρ 0 l} ∴ R = \frac{ρ 0 l}{2 π a}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
A solid cylinder of length l and cross-sectional area A is made of a material whose resistivity depends on the distance r from the axis of the cylinder as $ρ = k / r^{2}$ where k is constant . The resistance of the cylinder is -
A $\frac{π k l}{A^{2}}$
B $\frac{2 π k l}{A^{2}}$
C $\frac{π k l}{A}$
DNone
Question 2 - Select One
A current i passes through a wire of length l , radius of cross-section r and resistivity $ρ$ . The rate of heat generation is
A $\frac{i^{2} l ρ}{π r^{2}}$
B $i^{2} {(\frac{l ρ}{π r^{2}})}^{2}$
C $i^{2} l ρ / r$
D $i l ρ / r$
Question 3 - Select One
The hollow cylinder of length l and inner and outer radius $R_{1}$ and $R_{2}$ respectively. Find resistance of cylinder if current flows radially outward in the cylinder. Resistivity of material of cylinder id $ρ$ .
A $((\frac{ρ}{π e l} ln (\frac{R_{1}}{R_{2}}))$
B $((\frac{ρ}{4 π e l} ln (\frac{R_{2}}{R_{1}}))$
C $((\frac{ρ}{3 π e l} ln (\frac{R_{2}}{R_{1}}))$
D $((\frac{ρ}{2 π e l} ln (\frac{R_{2}}{R_{1}}))$

Recommended Questions

Home
Ask Doubt
Profile