A hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angel made by the radius through the block with the vertical is θ, find the angular speed at which the bowl is rotating.Solution in Tamil
Suppose the angular speed of rotatioin of the bowl is ω. The block also moves with this angular speed. The forces on the block are ure.
a. the normal force N and
b. the weight mg
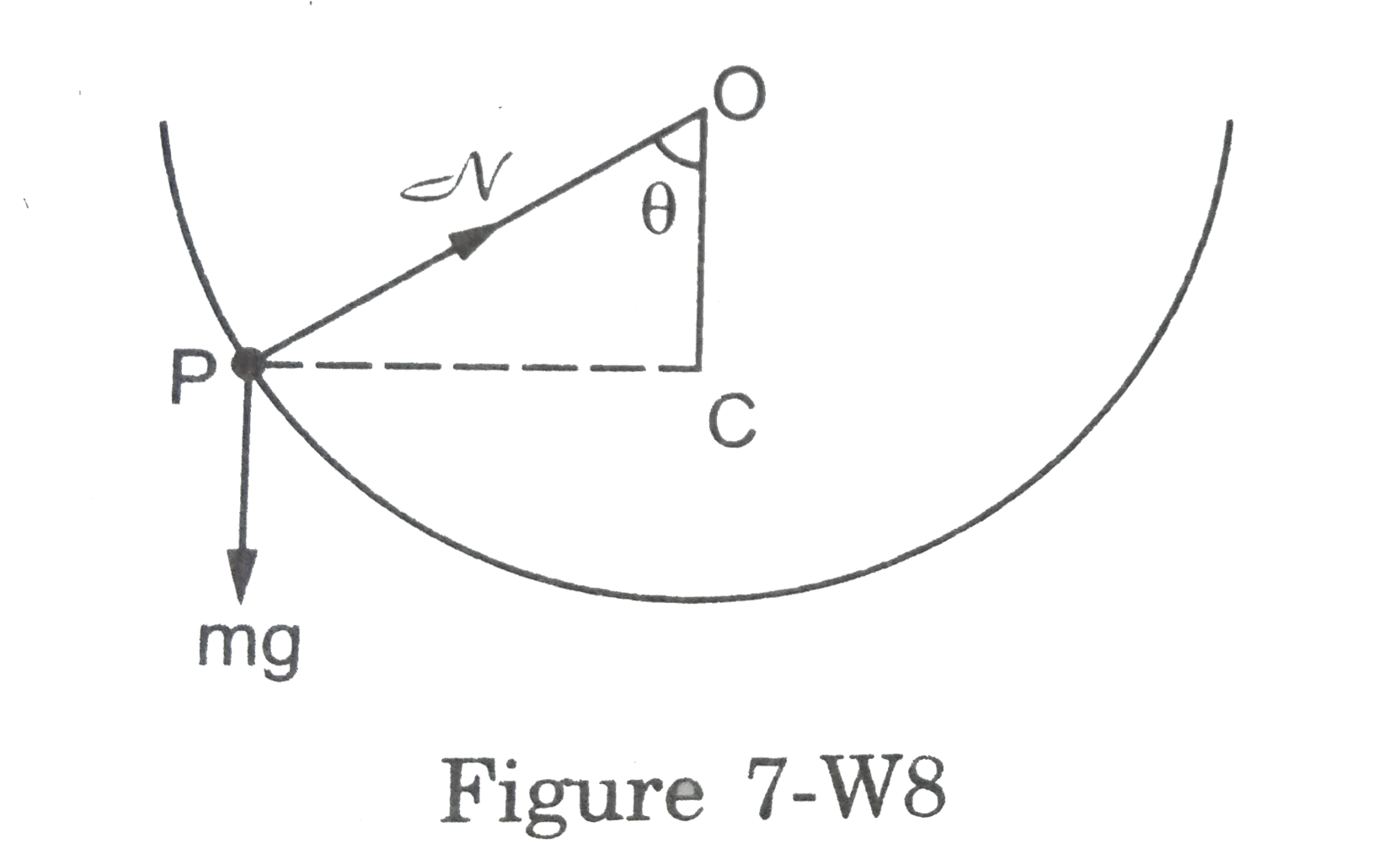
The block moves in a horizontal circle with the centre at C, so that teh radius is PC=OP sinθ=Rsinθ. Its acceleration is therefore ω2Rsinθ. Resolving the forces along PC and applying Newton's second law,
Nsinθ=mω2Rsinθ
or,N=mω2R ........i
As there is vertical acceleration,
Ncosθ=mg..........ii
Dividing i by ii
1cosθ=ω2Rg
or, ω=√gRcosθ
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer10videos
CIRCULAR MOTION
- BOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Objective -116videos
CIRCULAR MOTION
- BOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises30videos
CIRCULAR MOTION
- BOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises64videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - All Questions96videos
FLUID MECHANICS
Similar Questions
You are driving a motorcycle ona horizontal raod. It is moving with a uniform velocity. Is it possibel to accelerate the motorcycle wilthout putting higher petrol input rate into the engine?
01:52View SolutionWhen a particle moves in a circle with a uniform speed
08:55View SolutionFind the accelerationof the moon with respect to the eath from the following data, Distance between the earth and the moon =3.85×105 km and the time taken by the moon to complete one revolution around the earth =27.3days
02:34View SolutionThree particles of masses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
04:17View SolutionWater is filled in a flask up to a height of 20 cm. The bottom of the flask is circular with radius 10 cm. If the atmospheric pressure is 1.01×105 Pa, find the force exerted by the water on the bottom. Take g=10ms−2 and density of water =1000 kgm^-3.
06:30View SolutionA hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is5 cm. Find the outer curved surface area of the bowl.
03:20View SolutionA hemisphericla bowl of rdius R is rotated about its axis of symetry which is kept vertical.A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rottes with the bowl without any sliping. The friction coefficient between the block and teh bowl surface is μ. Find the range of the angular speed for which the block will not slip.
View SolutionA small mass of 10 g lies in a hemispherical bowl of radius 0.5 m at a height of 0.1 m from the bottom of the bowl. The mass will be in equilibrius if the bowl rotates at an
View SolutionA hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical A small block kept in the bowl rotates with the bowl without slipping on its surface If the surface of bowl is smooth and angle made by radius through the block with the vertical is 0 find the angular speed at which the bowl is rotating .
View SolutionA block is kept inside a hemispherical bowl rotating with angular velocity omega . Inner surface of bowl is rough, coefficient of friction is mu . The block is kept at a position where radius makes an angle theta with the vertical. What is the range of the angular speed for which the block will stay at the given position?
View SolutionA hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
05:04View SolutionA spherical bowl of radius R rotates about the verical diameter with angular velocity omega .The bowl contains a small object inside and in absence of friction, this object takes up a position inside the bowl such that its radius vector makes an angle theta with the vertical (see figure). Then
04:28View SolutionA hemispherical bowl of radius 0.1m is rotated about a vertical axis passing through the centre of the bowl with an angular velocity omega . A particle of mass m = 10^(-2) kg placed inside the bowl also the particle from the bottom of the bowl is h, find the relation between h and omega .
08:18View SolutionA hemispherical bowl of radius r is rotated with an angular velocity omega about a vertical axis passing through its centre. An object with the same angular velocity remaining attached with the inner surface of the bowl. The straight line joining the body and the centre of the bowl makes an angle 45^(@) with the vertical. The coefficient of friction between the body and the bowl is 0.2, Assuming the body is just about to move down along curved surface of the bowl, prove that omega^(2) r = 0.943 g.
View SolutionA hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surface of bowl is smooth, and the angle made by the radius through the block with the vertical is q, the angular speed at which the bowl is rotating is
View SolutionA hemispherical bowl of radius (R) is set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with bowl without slipping on its surface. If the surface of bowl is smooth, the angle made by the radius through the block with the vertical is θ. the angular speed at which the bowl is rotating
03:12View Solution

