Question

A block of mass m is suspended through a spring of spring constant k and is in equilibrium. A sharp blow gives the block an initial downward velocity v. How far below the equilibrium position, the block comes to an instantaneous rest?

Explanation

Klet us consider the blockthe spring+the earth as the system. The system has gravitatioN/Al potential energy corresponding to the force between the block and the earth as well as the elastic potential energy corresponding to the sring force. The total mechanicla energy includes kinetic enegy, gravitatioN/Al potential energy and elastic potential energy.

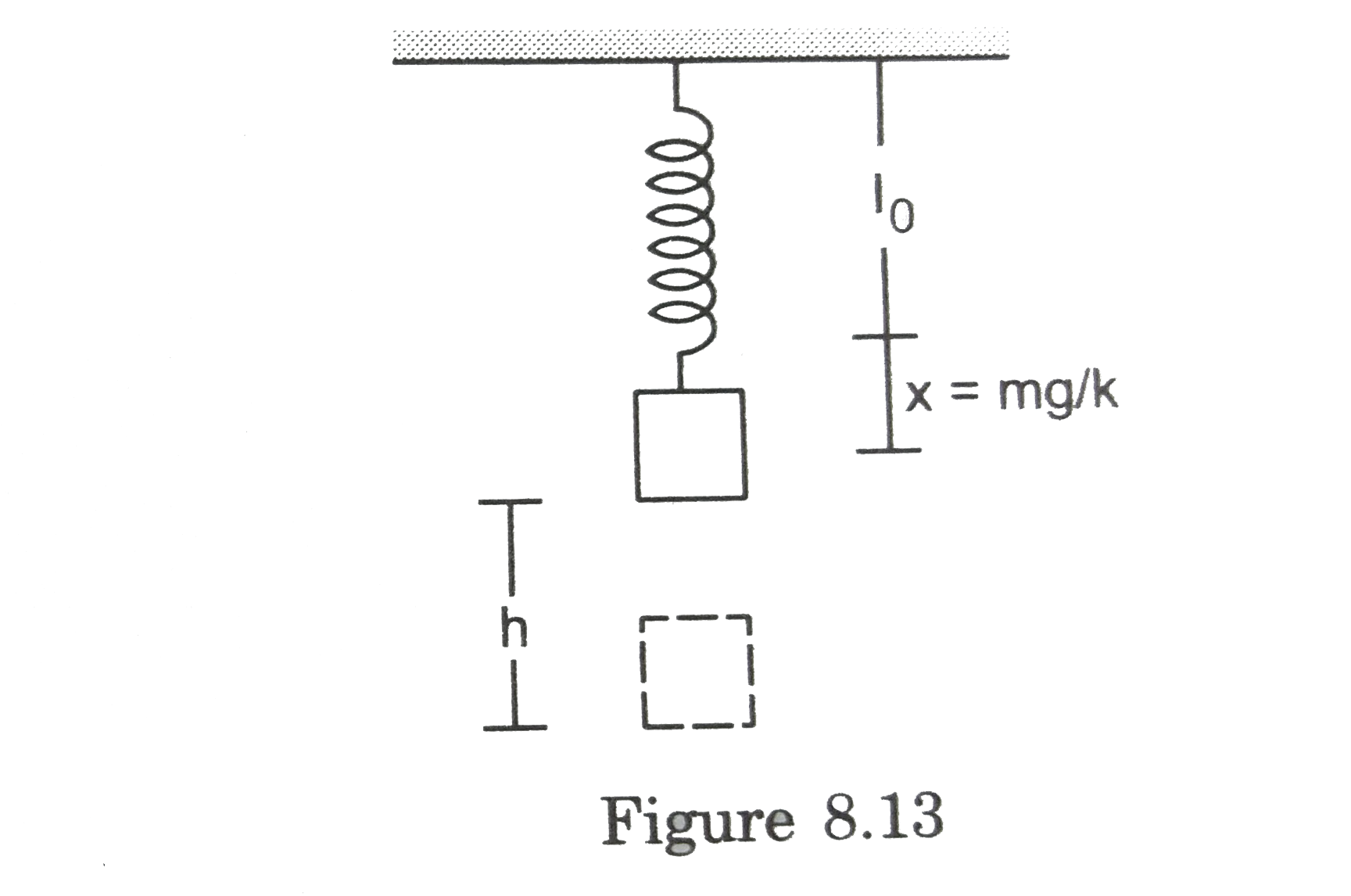
When the block is in equilibrium it is acted upon by two forces, a. the force of gravity mg and b. the tension in the spring `T-kx`. where x is the elongation. For equilibrium, mg=kx, so that the spring is stretched by a length `x=mg/k. The potential energy of the spring in this position is
`1/2 k(mg/k)^2=(m^2g^2)/(2k)`
Take the gravitatioN/Al potential energy to be zero in this position.. The total mechanicla energy of the system just after the blow is
`1/2 mv^2+(m^2g^2)/(2k)`
The only exterN/Al force on this system is that due to the ceiling which does no work. Hence, the mechanical energy o this system remains constant. If the block descends through a height h before coming becomes
`1/2k9mg/k+h)^2` and the gravitatioN/Al potential energy -mgh. the kineticenergy is zero is this state. Thus we have
`1/2mv^2+(m^2g^2)/(2k)=1/2k(mg/k+h)^2-mgh`
Solving this we get,
`h=vsqrt(m/k)`
Compare this with the result obtained in example. If we neglect gravity and consider the length of the spring in equilibrium position as the N/Atural length, the answer is same. This simplication is often used while dealing with vertical springs.