Question

A sphere rolls down an inclined plane of inclination $\theta$. What is the acceleration as the sphere reaches bottom ?

Explanation

Suppose the radils f the sphere is r. The forces acting on the sphere are shown in ure. They are a weight mg, b. normal force N and c. friction f.

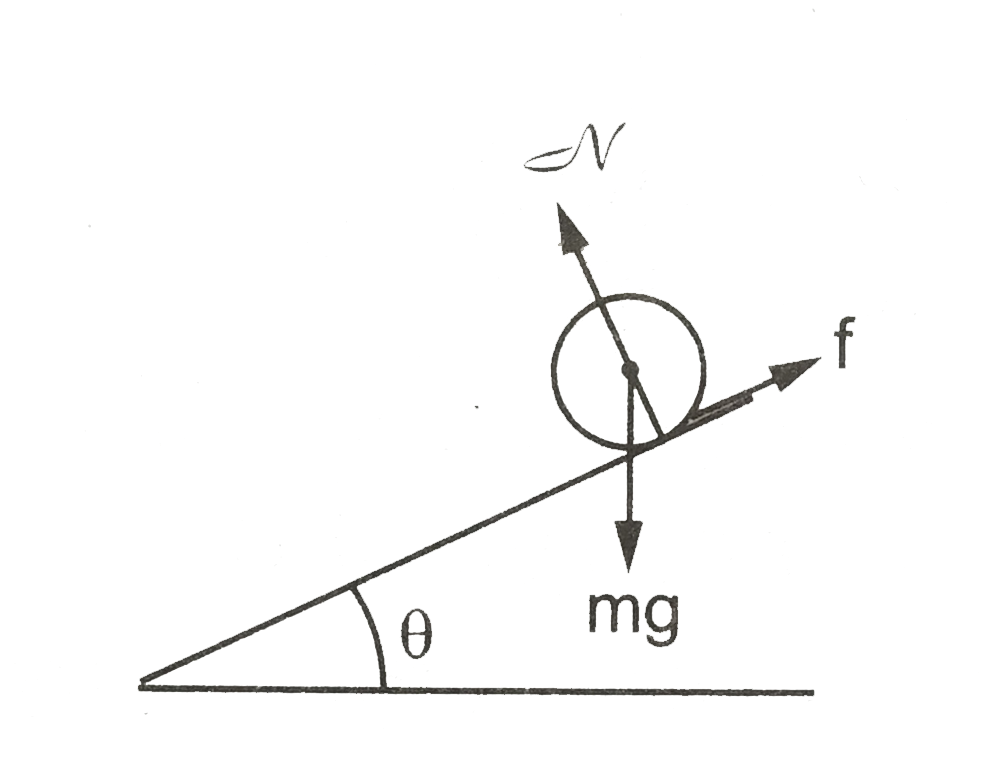
Let the linear acceleration of the sphere down the plane be a. The equation for the linear motion of the centre of mass is
`mg sintheta-f=ma`.............i
As the sphere rolls without slipping, its angular acceleration about the centre is `a/r. The equation of rotatioN/Al motion about the centre of mass is
`fr=(2/5mr^2)(a/r)`
or,` f=2/5ma`............ii
from i and ii
`a=5/7g sin theta`
and f=2/7 mg sintheta`
The normal force is equal to `mgcostheta` as there is no acceleration perpendicular to the incline. The maximum friction that can act is therefore, `mucostheta, where mu` is the coefficient of static friction. Thus, for pure rolling
`mucosthetagt2/7mg sintheta`
or `mugt2/7tantheta`