Figure shows two cylinders of radii r1andr2 having moments of inertia I1andI2 about their respective axes. Initially the cylinders rotate about their axes with angular speed ω1andω2 as shown in the figure. The cylinders are moved closer to touch each other keeping the axes parallel. The cylinders first slip over each other at the contact but the slipping finally ceases due to the friction between them. Find the angular speeds of the cylinders after the slipping ceases.
 Solution in Tamil
Solution in Tamil
When slipping ceases, the linear speeds of the points of contact of the two cylinders will be equal. If the ω1andω2 be the respective angular speeds, we have
ω'1r1=ω'2=r2……….i
The change in the angular speed is brought about by the frictioN/Al force which acts as long as the slipping exists. If this force f acts for a time t, the torque on the first cylinder is _1 and that on the second is _2. Assuming ω1r1>ω2r2 the corresponding angular impluses are −_1tand_2t. We therefore have
−_1t=I1(ω'1−ω1)
and_2t=I2(ω'2=ω2)
or −I1r1(ω'1−ω1)=I2r2(ω'2−ω2)........ii
Solving i and ii
ω'1=I1ω1r2+I2ω2r1I2r21+I1r22r2andω'2=I1ω1r2+I2ω2r1I2r21+I1r22
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
22 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -1
26 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
Can an object be in pure translation as well as in pure rotation?
View SolutionLet →A be a unit vector along the axis of rotation of a purely rotating body and →B be a unit vector along the velocity of a particle P of the body away from the axis. The value of →A.→B is
View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration.
View SolutionA man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
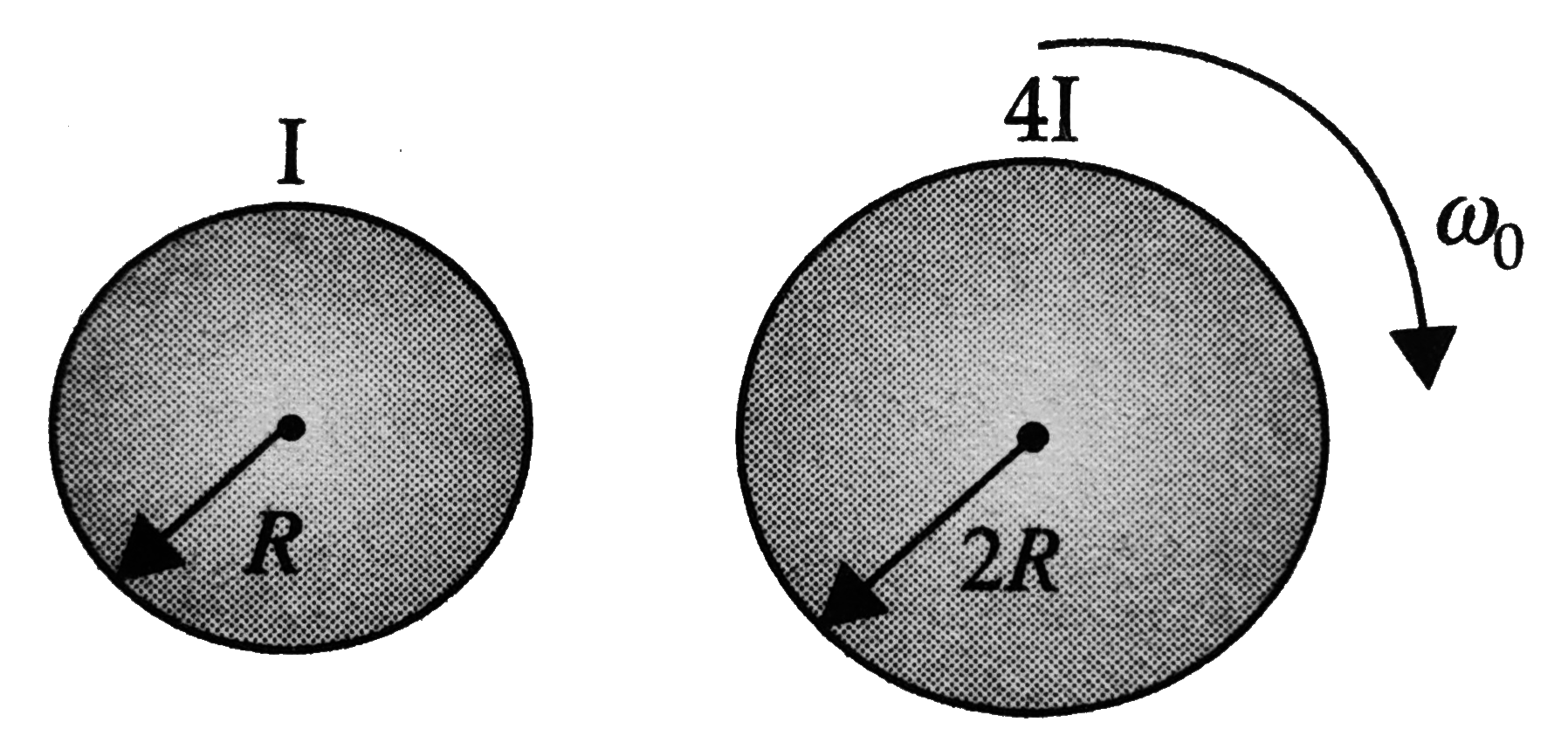
View SolutionTwo cylinders having radii 2R and R and moment of inertia 4I and I about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity ω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
View SolutionTwo discs of moments of inertia I_1 and I_2 about their respective axes, rotating with angular frequencies, omega_1 and omega_2 respectively, are brought into contact face to face with their axes of rotation coincident. The angular frequency of the composite disc will be A .
View SolutionTwo horizontal discs A and B of radii r and 2r having moments of inertia I and 4I about their axes. Initially, disc A is rotating with ω0 and disc B is at rest. Their rims are now brought in contact. The discs first slip over each other at the contact but slipping finally ceases due to the fricition between them. Find the angular speeds of the discs after the slipping ceases. Also, find the loss in kinetic energy.
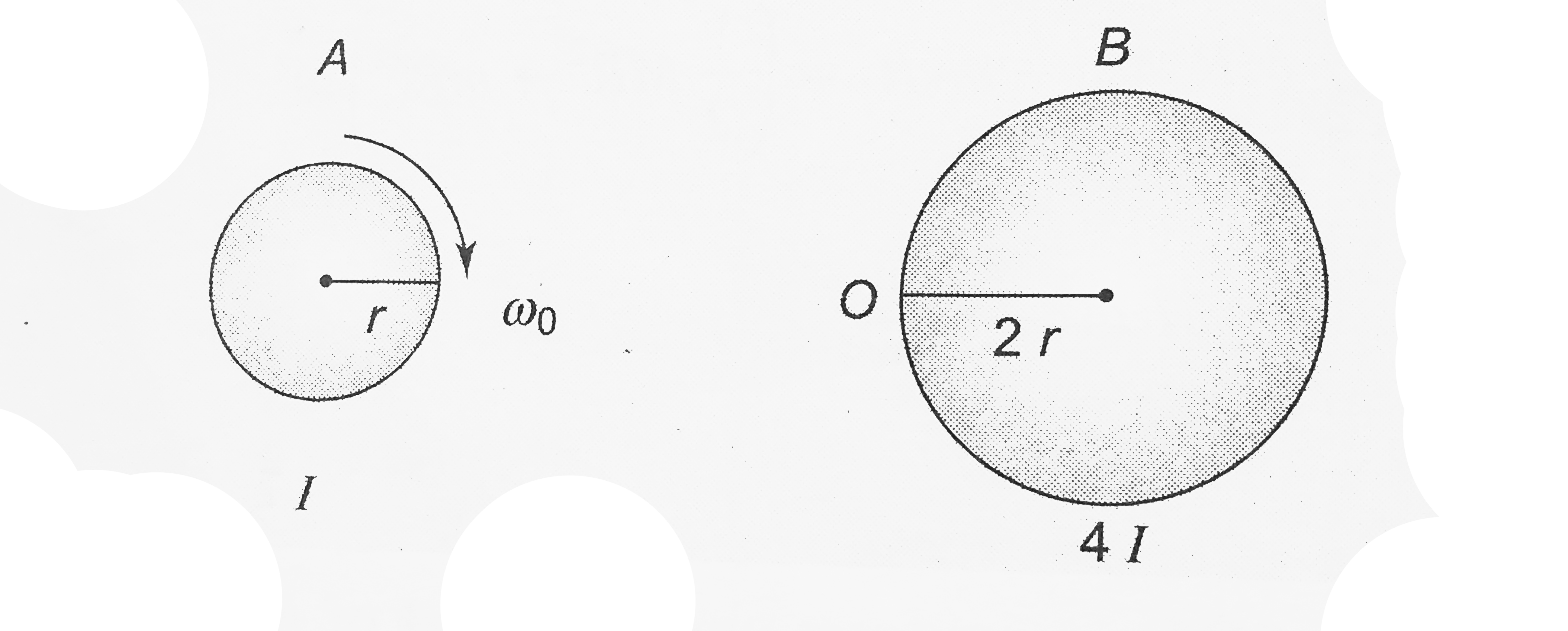
View SolutionThe axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed v_(1) . It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I For the entire process the quantitiy (ies) which will remain conserved for the (cylinder+block) system is/ are (anuglar momentum is considered about the cylinder axis)
View SolutionThe axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed v_(1) . It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I If omega is final angular velocity of the cylinder, then
View SolutionTwo cylinders with radii r1 and r2 and rotational inertia I1 and I2 are supported on their horizontal axles. The first one is set in rotation with angular velocity ε. The axle of the other cylinder (smaller) is moved until it touches the large cylinder and is caused to rotate by the frictional forces between the two. Find the angualr velocity of the two cylinders after slipping ceases between them.
[Hint: Consider angular impulse received by the cylinders]
View SolutionTwo cylinders having radiii R_(1) and R_(2) and rotational inertia I_(1) and I_(2) respectively, are supported by fixed axes perpendicular to the plane of figure-5.52. The large cylinder is initially rotating with angular velocity omega_(0) . The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually, slipping ceases, and the two cylinders rotate at constant rates in opposite directions, (a) Find the final angular velocity omega_(2) of the small cylinder in terms of I_(1) , I_(2) , R_(1) , R_(2) and omega_(0) . (b) Is total angular momentum conserved in this case ?
View SolutionTwo thin planks are moving on a four identical cylinders as shown. There is no slipping at any contact points. Calculate the ratio of angular speed of upper cylinder to lower cylinder

View SolutionTwo discs of moments of inertia I1 and I2 about their respective axes , rotating with angular frequencies ω1 and ω2 respectively, are brought into contact face to face with their axes of rotation coincident. The angular frequency of the composite disc will be
View Solution(A) : Two solid cylinders of different masses and radii take same time to roll down an inclined plane without slipping.
(R ) : Moment of inertia of two solid cylinders of different masses and radii about their natural axes are different.
View SolutionTwo discs of moments of inertia I1 and I2 about their respective axes , rotating with angular frequencies ω1 and ω2 respectively, are brought into contact face to face with their axes of rotation coincident. The angular frequency of the composite disc will be
View Solution
