A force F acts tangentially at the highest point of a sphere of mass m kept on a rough horiozontal plane. If the sphere rolls withut slipping, find the accelerastioni of the centre of the sphere. Solution in Tamil
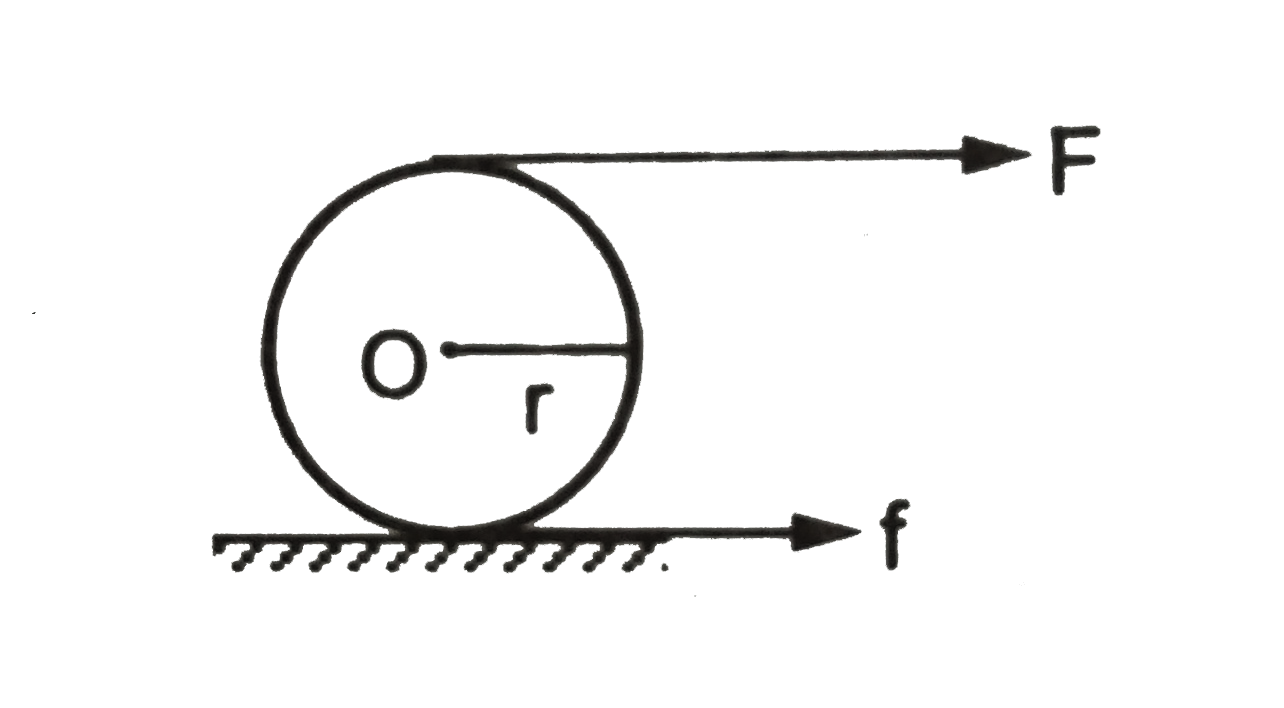
The situation ikn shown in ure. As the force F rotates the sphere , the point of contact has a tendency to slip twoards left sothat the static friction on the shre will act towards rith. Let r be the radius of hte sphere aN/A be the linear accelerastion about the centre of the sphere is α=ar as there is no centre
F+f=ma...........i
andtherotatioNAlmot∈aboutthecentre<br>Fr-fr=Ialpha=2/5 mr^2)(a/r)<br>or F-f=2/5ma.......ii<br>from i and ii
2F=75maor,a=10F7m.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer22videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -126videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises86videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises51videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises58videos
SIMPLE HARMONIC MOTION
Similar Questions
Can an object be in pure translation as well as in pure rotation?
09:46View SolutionLet →A be a unit vector along the axis of rotation of a purely rotating body and →B be a unit vector along the velocity of a particle P of the body away from the axis. The value of →A.→B is
09:45View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration.
02:39View SolutionA man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
05:06View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
06:51View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M . The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.
View SolutionA force F acts tangentially at the highest point of a disc of mass m kept on a rough horizontal plane. If the disc rolls without slipping, the acceleration of centre of the disc is:
 04:09View Solution
04:09View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If mass of the sphere is m and its radius be R, then the angular momentum of the sphere about the point of contact is.
03:17View SolutionA force F acts tangentially at the highest point of a solid cylinder of mass m kept on a rough horizontal plane. If the cylinder rolls without slipping, find the acceleration of the center of cylinder.
07:23View Solution
A solid sphere of mass ma nd radis R is placed on a rough horizontal surface A horizontal force F is applied to sphere at a height h, (0≤h≤R) from centre. If sphere rolls slipping then,06:44View SolutionA solid sphere of radius R is rolled by a force F acting at the topo of the sphere as shown in the figure. There is no slipping and initially sphere is in the rest position, then (CM= centre of mass)
 07:49View Solution
07:49View SolutionA solid sphere of mass 2kg is pulled by a constant force acting at its centre on a rough surface having co-efficient of friciton 0.5. The maximum value of F so that the sphere rolls without slipping is
 04:09View Solution
04:09View SolutionA solid sphere of radius R and mass M is rolled by a force F acting at the top of the sphere as shown in the figure. The sphere starts from rest and rolls without slipping, then
 04:13View Solution
04:13View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is
 03:09View Solution
03:09View SolutionA sphere of mass m rolls without slipping on an inclined plane of inclination θ. Find the linear acceleration of the sphere and the force of friction acting on it. What should be the minimum coefficient of static friction to support pure rolling?
04:25View SolutionA solid sphere of radius R is rolled by a force F acting at the topo of the sphere as shown in the figure. There is no slipping and initially sphere is in the rest position, then (CM= centre of mass)
04:15View Solution

