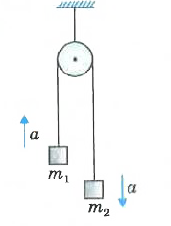
Two masses M and m are connect by a light string gong over a pulley of radis r. The pulley is free to rotate about its axis which is kept horizontal. The moment of inertia of the pulley about the axis is I. The system is releaed from rest. Find the angular momentum fo teh system when teh mass Mhas descended through a height h. The string does not slip over the pulley.Solution in Tamil
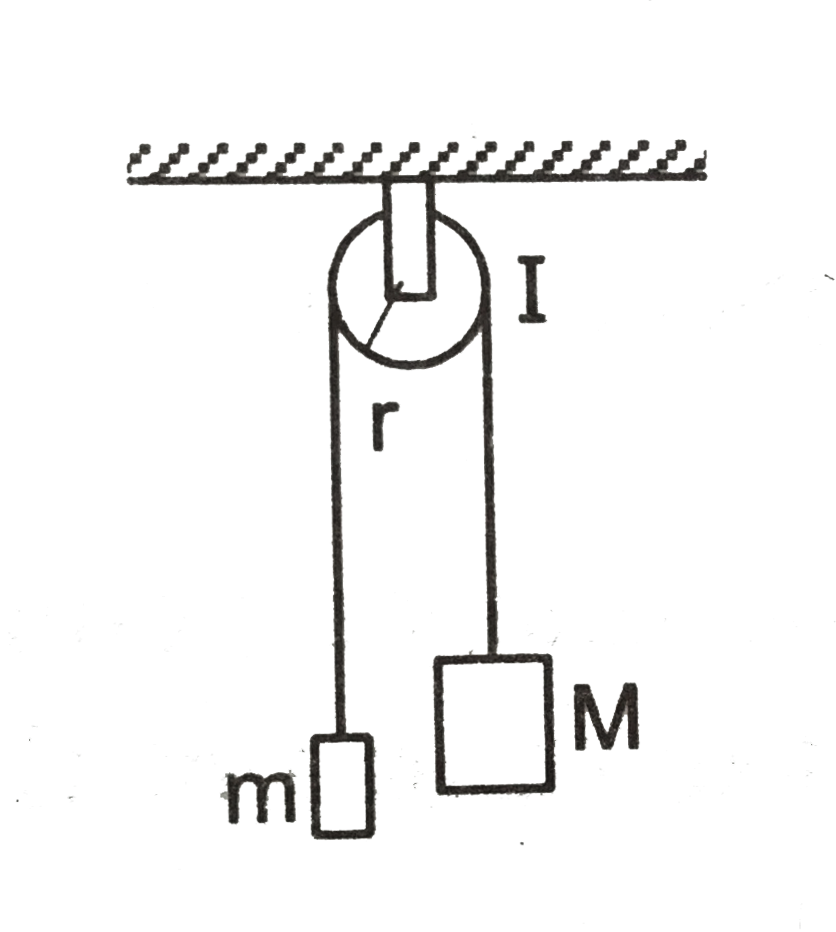
The situation is shown in ure. Let the speed of the masses be v at time t. This will also be the speed of a point on the rim of the wheel and hence the angular velocity of the wheel at time t will be v/r. If the height descended by the mass M is h the loss in the potential energy of the mass plus the pulley system is mgh−mgh. The gain in kinetic energy is 12Mv2+12mv2+12I(vr)2. An no energy is lost,
12(M=m+1r2)v2=(M−m)gh
or,v2=2(M−m)ghM+m+1r2
The angular momentum of the mass M is Mvr and that of the mass is mvr in the same direction. The angular momentum of the pulley is Iω=Ivr. The total angular momentum is
[(M+m)r+Ir]v=[(M+m+Ir)r]
⎷2(M−m)ghM+m+Ir2
=√2(M−m)(M+M+1r2)r2gh
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer22videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -126videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises86videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises51videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises58videos
SIMPLE HARMONIC MOTION
Similar Questions
Can an object be in pure translation as well as in pure rotation?
04:56View SolutionLet →A be a unit vector along the axis of rotation of a purely rotating body and →B be a unit vector along the velocity of a particle P of the body away from the axis. The value of →A.→B is
07:58View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration.
View SolutionA man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
03:34View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
06:09View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
 09:07View Solution
09:07View SolutionFigure shows two blocks of masses m and M connected bky a string pasing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotte about this axis. Find the accelerationof the mass M asuming that the string does not slip on the pulley.
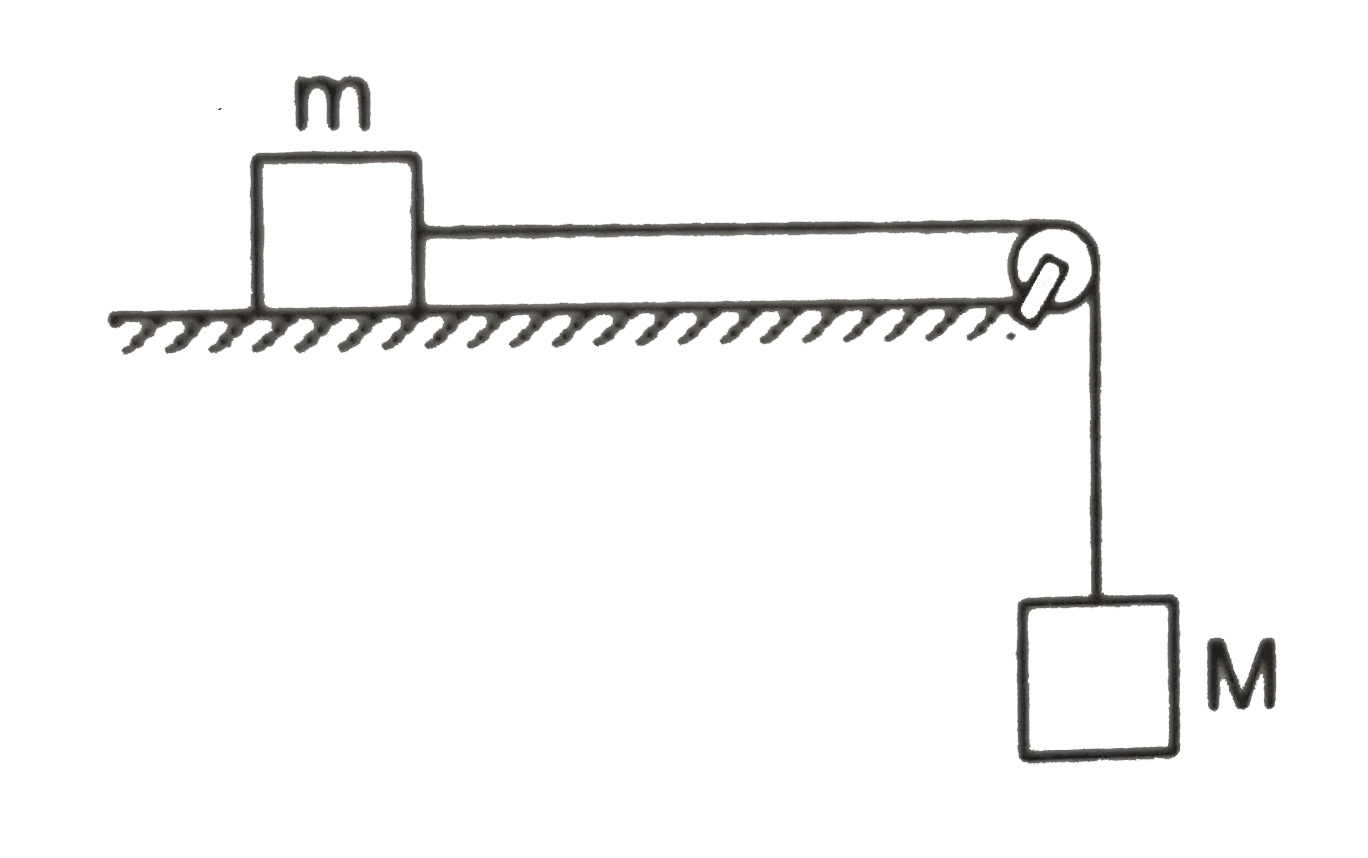 08:16View Solution
08:16View SolutionSolve the previous problem if the pulley has a moment of inertia I about its axis and the string does not slip over it.
14:27View SolutionA pulley has the shape of a uniform solid disc of mass 2kg and radius 0.5m. A string is wrapped over its rim and is pulled by a force of 2.5N. The pulley is free to rotate about its axis. Initially, the pulley is at rest. Find the angular velocity and angle rotated by pulley in 10s.
 04:32View Solution
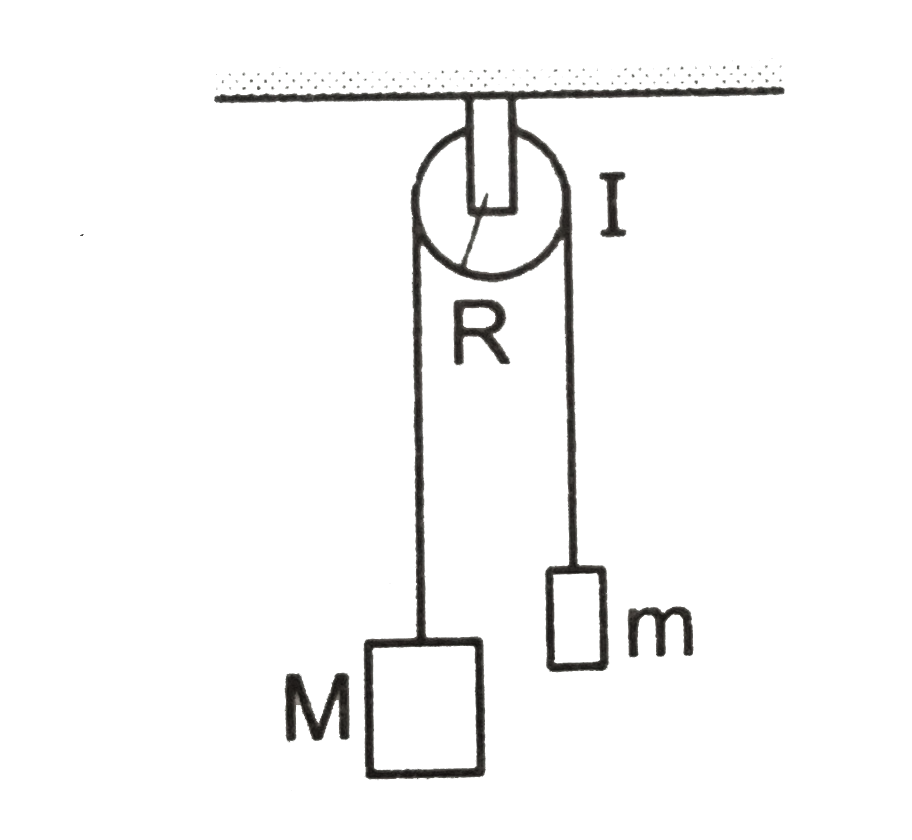
04:32View SolutionTwo blocks of masses 2m and m are connected by a light string going over a pulley of mass 2m and radius R as shown in the figure. The system is released from rest. Find the angular momentum of system when the mass 2m has descended through a height h. Assume no slipping.
 04:46View Solution
04:46View SolutionSystem is released from rest. Moment of inertia of pulley 'I'. Find angular speed of pulley when m_1 block falls by 'h'. (Given m_1 gt m_2 and assume no slipping between string and pulley).
View Solutionदो द्रव्यमान m तथा M एक नगण्य भार वाली डोरी से बँधे है जो एक स्थिर घिरनी पर से होकर जाती है | घिरनी का अक्ष क्षैतिज है, इसकी त्रिज्या r है तथा अक्ष के प्रति इसका जड़त्व आघूर्ण I है | घिरनी की धुरी पर कोई घर्षण नहीं है तथा डोरी घिरनी पर फिसलती नहीं है | इस पुरे निकाय को स्वतंत्र रूप से गति करने के लिए छोड़ दिए जाता है | जब द्रव्यमान M, h दुरी निचे आता है, उस समय घूर्णन अक्ष के प्रति निकाय का कोणीय संवेग ज्ञात करें |
04:52View Solutionदो द्रव्यमान तथा M एक घिरनी पर से होकर गुजर रही एक रस्सी से जुड़ हुए है (चित्र 18.E4)। द्रव्यमान m चिकनी क्षैतिज टेबुल पर फिसलता है। घिरनी की त्रिज्या r है तथा अक्ष के परितः इसक जड़त्व आघूर्ण I है। यह अपने अक्ष के परितः मुक्त रूप से घूर्णन कर सकती है। यह मानते हुए कि घिरनी पर रस्सी फिसलती नहीं है, द्रव्यमान M का त्वरण ज्ञात करें
 04:13View Solution
04:13View SolutionFigure shows two blocks of mass m and m connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley (uniform disc) has mass m and it can freely rotate about this axis. Find the acceleration of the mass m assuming that the string does not slip on the pulley.
06:28View SolutionA string of negligible mass is wrapped on a cylindrical pulley of mass M and radius R. The other end of string is tied to a bucket of mass m. If the pulley rotates about a horizontal axis then the tension in the string is :
View SolutionString going over a pulley connects two blocks of masses m, and my. String and pulley are light. Calculate acceleration of centre of mass of blocks system.
 View Solution
View Solution

