Suppose the particle of the previous problem has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M. a. Find the velocity of the particle with respect to C of the system consituting the rod plus the particle. b. Find the velociyt of the particle with respect to C before the collision. c. Find the velocity of the rod with respect to C before the colision. e. find the moment of inertia of the system about the vertical axis through the centre of mass C after the collision. f. Find the velociyt of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.Solution in Tamil
The correct Answer is:A, B, C, D
a. Since mv=(M+m)v'
→v'=mvM+m

b. Velocity of the particle w.r.t C before the collision =v−v'
=v−mvM+m=MvM+v
c.Velocityoftherodw.r.tCbeforecollision<br>=-(Mv)/(M+m)<br>d. :. x_(cm)=(m_1x_1+m_2x_2)/(m_1+m_2)<br>=(ML)/(2(M+m))<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C10_E01_124_S02.pngwh=80%mx-autosty≤=background:white;><br>:.Anga––rmomentumofbody<br>=mvr<br>=m(Mv)/(M+m).(ML)/(2(M+m))<br>=(M^2mvL)/(2(M+m)^2)<br>:.Anga––rmomentumofrodaboutcm.<br>=M.(mv)/(M+m).1/2 m/(M+m)
=Mm2vL2(M+m)2
[∴r=12−ML2(M+m)=12mM+m]
e. M.I. =I1+I2
=−m[ML2(M+M)]2+ML212+M[ML2(m+M)]2
=mM2L24(m+M(]2+ML212+Mm2L24(M+m)□
=(3mM^2L^2+M(m+M)^2L^2+3Mm^2L^2)/(12(M+m))<br>=(M(M+4m)L^2)/(12(M+m))<br>f.wehav<br>V_(cm)=(mv)/(M+m)<br>:. Iw=mvr=m.v. (ML)/(2(M+m))<br>:.w=(MvML)/(2(M+m)).(12(M+m))/(M(M+4m)L^2<br>=(6mv)/((M+4m)L)
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -215videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises51videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises58videos
SIMPLE HARMONIC MOTION
Similar Questions
The axis of rotation of a purely rotating body
03:39View SolutionA man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
01:59View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
02:49View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
02:49View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M . A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the velocity of the centre of mass C of the system constituting 'the rod plus the particle'.
08:26View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M . A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the velocity of the particle with respect to C before the collision
10:20View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M . A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the velocity of the rod with respect to C before the collision
08:12View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M . A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the angular momentum of the particle and of then about the centre of mass C before the collision.
10:25View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.View SolutionA Iong slender rod of mass 2 kg and length m is placed on a smooth horizontal table. Two particles of masses 2 kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig. , If the two particles strike the rod in opposite direction, then after collision, as compared to the previous situation the rod will
05:10View SolutionA uniform rod of mass m and length l has been placed on a smooth table A particle of mass m, travelling perpendicular to the rod, hits it at a distance x = (l)/(sqrt6) from the centre C of the rod. Collision is elastic. (a) Find the speed of the centre of the rod and the particle after the collision. (b) Do you think there is a chance of second Collision? If yes, how is the system of particle and stick moving after the second collision?
05:55View Solutionमान ले कि प्रश्न 20 में कण का द्रव्यमान m तथा टक्कर से पूर्व इसकी चाल v है तथा टक्कर के पश्चात यह छड़ से चिपक जाता है। छड़ का द्रव्यमान M है।
(a) 'छड़ एवं कण ' इस निकाय के द्रव्यमान केंद्र C का वेग ज्ञात करे।
(b) टक्कर से पूर्व C के सापेक्ष कण का वेग ज्ञात करे।
(c) टक्कर से पूर्व C के सापेक्ष छड़ का वेग ज्ञात करे।
(d) टक्कर से पूर्व द्रव्यमान केंद्र C के सापेक्ष कण तथा छड़ के कोणीय संवेग ज्ञात कीजिए।
(e) टक्कर के पश्चात द्रव्यमान केंद्र C गुजरनेवाले ऊर्ध्वाधर अक्ष के परितः निकाय का जड़त्व आघूर्ण ज्ञात कीजिए।
(f) टक्कर के पश्चात द्रव्यमान केंद्र C का वेग तथा द्रव्यमान केंद्र के परितः निकाय का कोणीय वेग ज्ञात करे।03:16View SolutionA uniform rod of length λ lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out.
The moment of inertia of the system about the vertical axis passing through the centre of mass C after the collision.02:55View SolutionA uniform rod of length lambda lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out. The velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
05:26View Solution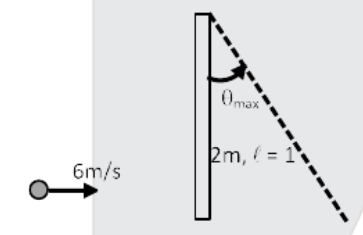
Find maximum angular displacement of rod. if particle sticks after collision.01:28View SolutionA particle of mass m is moving perpendicular to a rod of length L kept on a frictionless horizontal surface and collides at a distance L/4 from the centre of rod. Particle comes to state of rest just after collision. Mass of rod is M and speed of particle before collision is u. Let v is the velocity of centre of rod after collision and is angular velocity attained by the rod. Find (Lomega)/(v)
View Solution

