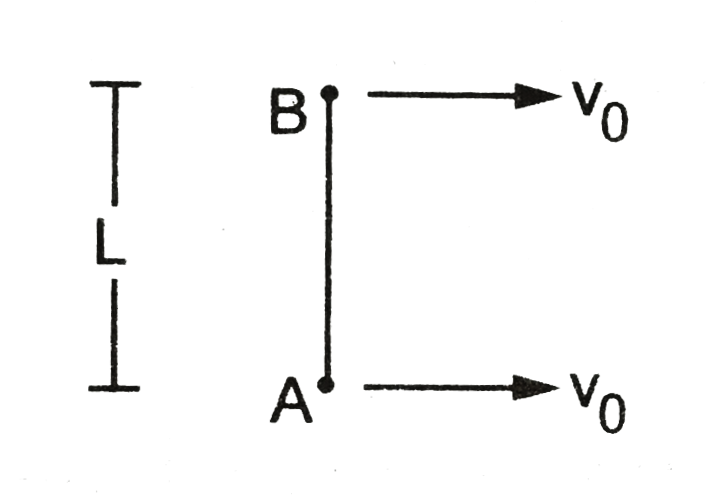
Two small balls A and B each of mass m, are joined rigidly to the ends of a light rod of length L figure. The system translates on a frictionless horizontal surface with a velocity v0 in a direction perpendicular to the rod. A particle P of mass kept at rest on the surface sticks to the ball A as the ball collides with it . Find
a. the linear speeds of the balls A and B after the collision, b. the velocity of the centre of mass C of the system A+B+P and c. the angular speed of the system about C after the collision.
 Solution in Tamil
Solution in Tamil
The correct Answer is:A, B, C, D
Two ball A and B each of mass m are joined rigidly to the ends of a light rod of length L. The system moves with a velocity V0 in a direction perpendicular to the rod. A particle P of mass m kept at rest rod. A particle OP of masss m kept at rest on teh surface sticks to the ball A as the ball collides with it.
a. The light rod wil exert a force on the bal B only along its length. So collision will not affect its velocity.
B has a velocity =V0
if we consider the three bodies to be a system
Applying L.C.L.M.
Therefore mv0=2m×v
→v=v02
Therefore A has velocity =v02
b. If we consider the three bodies tobe a system
net exterN/Asl force =0<br>Therefore<br>V_(VCM)=(mxxv_0+2mxx(v_0/2))/(m+2m)<br>>=(mv_0+mv_0)/(3m)<br>=(2v_0)/3<br>(alongthe∈i<ialvelocityasbefoecollision)<br>c.Thevelocityof(A+P)w.r.t<br>the center of pass ={((2v_0)/3)}-(v_0-2)<br>=v_0/6<br>andthevelocityofBw.r.tthecentreofmass<br>=v_0-(2v-0)/3=v_0/3<br>(onlymagnitudehasbeentaken)<br>Distanceofthe(A+P)omcentreofmass<br>=l/3 and for B it is ((2l)/3)<br>therforeP_(cm)=L_(cm)xxomega<br>rarr 2mxxV_0/6xxl/3+mxxV_0/3xx(2l)/3
{2m(l3)2+(2l3)2m}×ω
rarr 6m(V_0l)/18=18((6ml)/9)omega<br>rarr omega=(v_0/(2l))
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -2
15 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
The axis of rotation of a purely rotating body
View SolutionA man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
View SolutionA rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m traveling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision the particle comes to rest. Find the ration m/M.
View SolutionA uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View SolutionTwo small balls A and B, each of mass m, are joined rigidly at the ends of a light rof of length L. they are placed on a frictionless horizontal surface another ball of mass 2 m moving with speed u towards one of the ball and perpendicular to the length of the rod on the horizontal frictionless surface as shown int he figure. if the coefficient of restitution is 1/2 then the angular speed of the rod after the collision will be
View SolutionA rod of mass m and length l is kept on a surface that has no friction. If a ball comes & hits the lower end with a velocity v, then the velocity of centre of mass will be
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
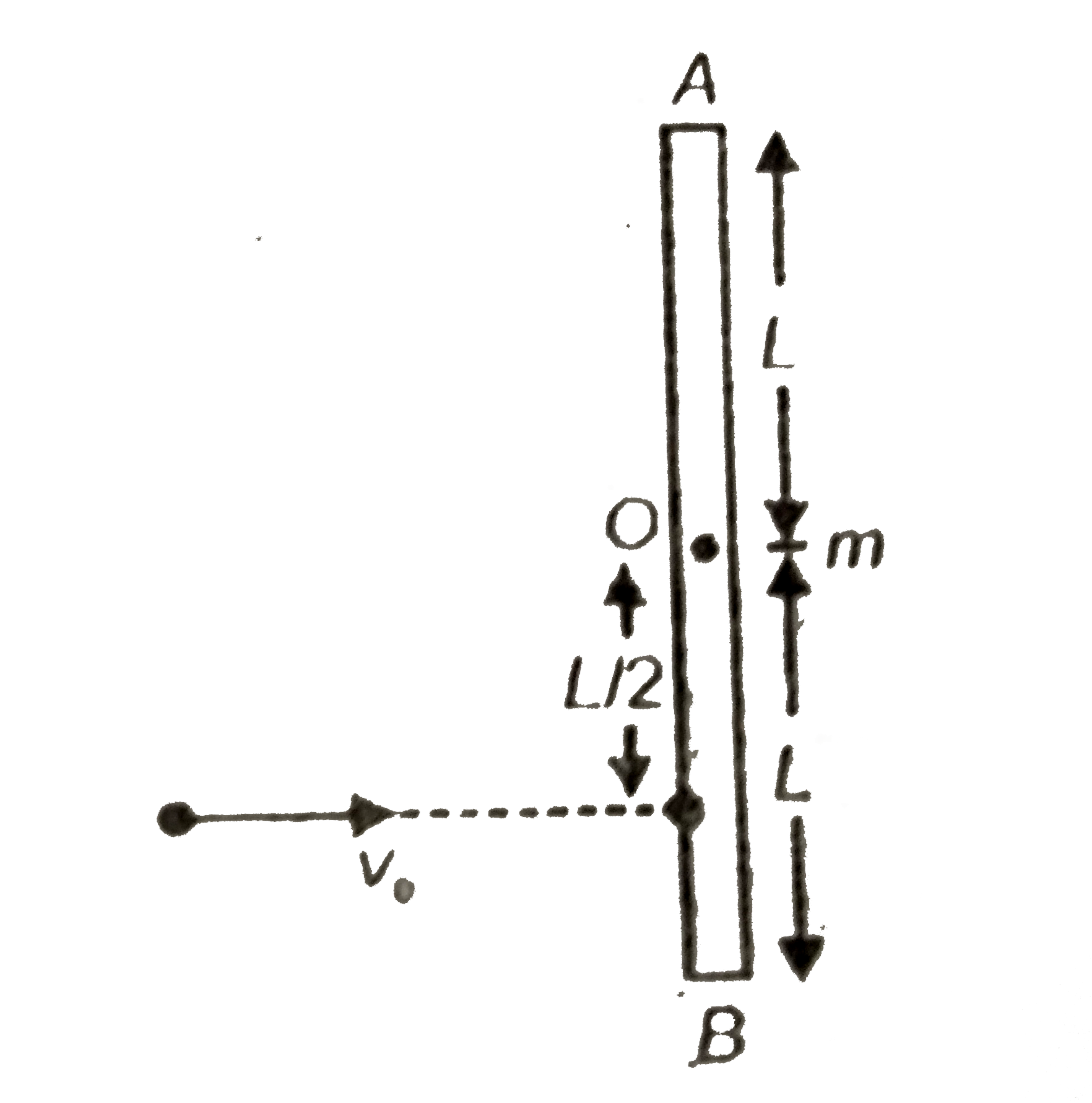
Angular velocity of rod just after collision is
View SolutionA stick of length L and mass M lies on a frictionless horizontal surface on which it is free to move in any way. A ball of mass m moving with speed v collides elastically with the stick as shown in the figure. If after the collision the ball comes to rest, then what would be the mass of the ball?

View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View SolutionA rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View SolutionA stick of length L and mass M lies on a frictionless horizontal surface on which it is free to move in any way. A ball of mass m moving with speed v collides elastically with the stick as shown in the figure. If after the collision the ball comes to rest, then what would be the mass of the ball?

View SolutionTwo small balls A and B, each of mass m are joined rigidly by a light horizontal rod of length L. The rod is clamped at the centre in such a way that it can rotate free about a vertical axis through its centre. The system is rotated with an angular speed ω about the axis. A particle P of mass m kept at rest sticks to the ball A as the ball collides with it. The new angular speed of the rod is yω/3 then value of y.
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.

Angular velocity of rod just after collision is
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.

Angular velocity of rod just after collision is
View SolutionA rod of mass m and length l is kept on a surface that has no friction. If a ball comes & hits the lower end with a velocity v, then the velocity of centre of mass will be

View Solution
