Suppose the rod with the balls A and B of theprevious problem is clamped at the centre in such a way that it ca rotate freely about a horizontal axis through the clamp. The system is kept at rest in the horizontal position. A particle P of the same mass m is dropped from a heigh h hon the ball B. The particle collides with B and sticks to it. a. Find the angular momentum and the angular speed of the system just after the collision. b. What should be the minimum value of h so that the system makes a full rotation after the collision.Solution in Tamil
The correct Answer is:A, B, C
a. Angular momentum =mvr
conservation of linear momentum
μ=2mv−mv=mv
∴u=v=mvr
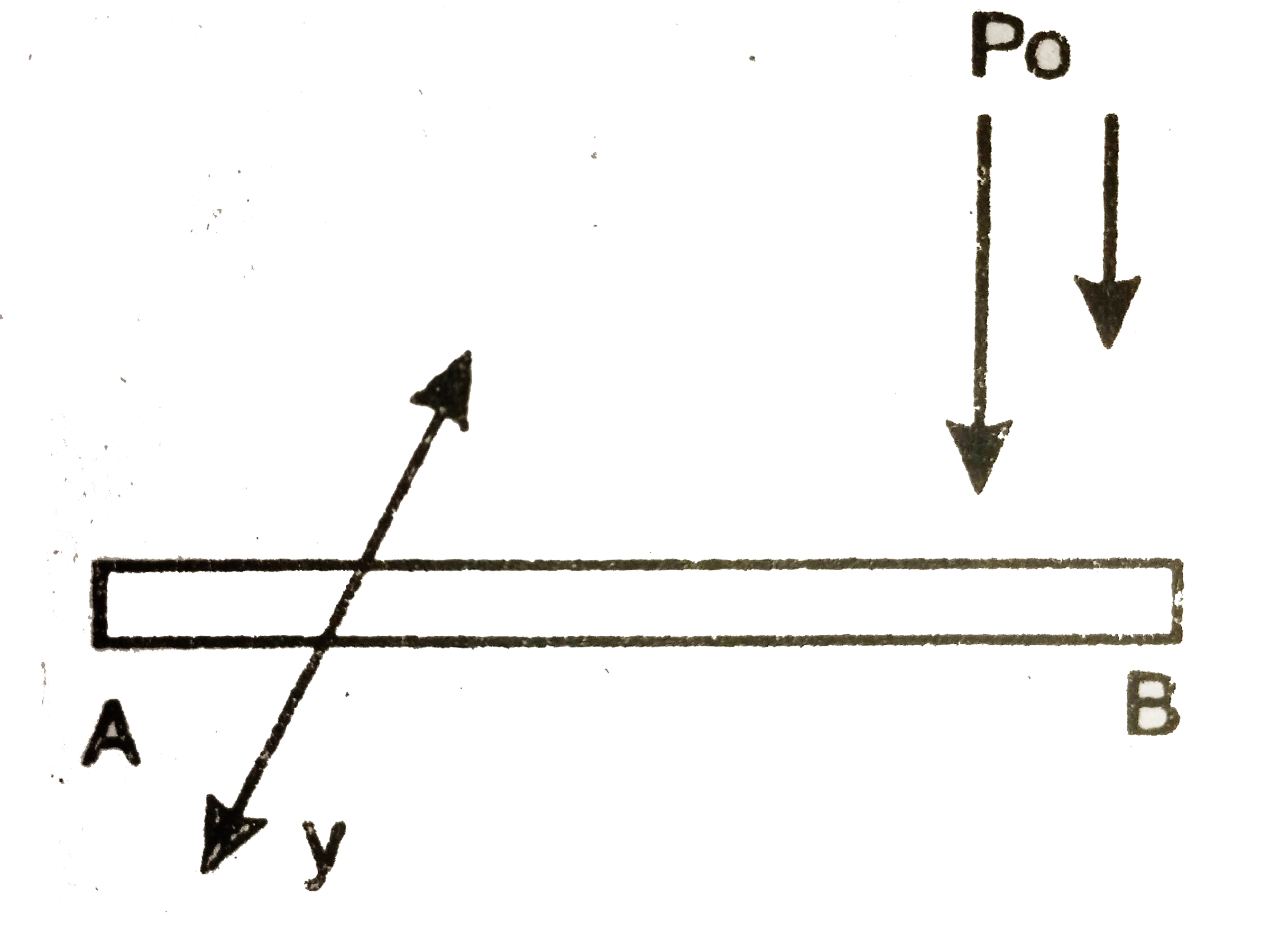
Velocity =sqrt(2gh)<br>andr=L/2<br>Angular momentum =m.sqrt(2gh.L/2<br>=(mLsqrt(gh))/sqrt2<br>Anga––rmomentum=lw<br>:.omega=angular velocity =L/I<br>or=I=(2mL^2)/4+(mL^2)/4=(3mL^2)/4<br>:. omega=(mLsqrtI(gh)/sqrt2)/(3mL^2/4)=sqrt(8gh)/(3L)<br>b.Whenthemass2mwilbeatthe⊤mostpositionandthemassmbetˆthelowestp∮.Theywillau→maticalyrotate.<br>∈thispositionthe→talgaion∈potentiale≠rgy<br>=2mgxx(L/2)-mg(L/2)<br>∴mgL/2=((1/2x2mL^2))/4xx((8gh)/(9gL^2))<br>rarr h=(3L)/2
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -215videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises51videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises58videos
SIMPLE HARMONIC MOTION
Similar Questions
The axis of rotation of a purely rotating body
03:16View SolutionA man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
04:49View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
17:56View SolutionTwo small bals A and B, each of mass m, are joined rigidlyl by a light horizontal rol of lengh L. The rod is clasmped at the centre in such a way that it c an rotate freely about a verticl axis through its centre. The systemis rotated with an angualr speed ω about the axis. A particle P of masss m kept at rest sticks to the ball A as the ball collides with it. Find the new angular speed of the rod.
05:15View SolutionTwo small balls A and B each of mass m, are joined rigidly to the ends of a light rod of length L figure. The system translates on a frictionless horizontal surface with a velocity v0 in a direction perpendicular to the rod. A particle P of mass kept at rest on the surface sticks to the ball A as the ball collides with it . Find
a. the linear speeds of the balls A and B after the collision, b. the velocity of the centre of mass C of the system A+B+P and c. the angular speed of the system about C after the collision.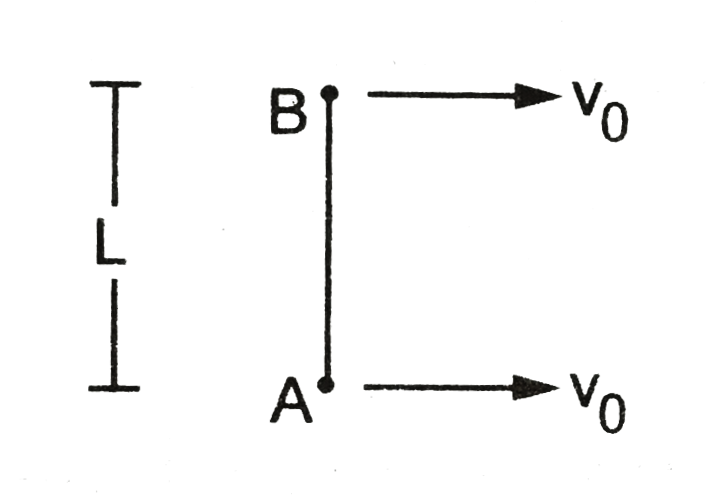
06:42View SolutionA metre stick weighing 240 g is pivoted at its upper end in such a way that it can freely rotate in a vertical plane through this end figure. A particle of mass 100 g is attached to the upper end of the stick through a light sting of length 1 m. Initially the rod is kept veritcal and the string horizontal when the system is released from rest. The particle colides with the lower end of the stick and sticks there. Find the maximum angle through which the stick will rise.
04:37View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity omega . A particle of same mass m and having velocity of 2omegaR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
17:47View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity omega . A particle of same angular velocity mass m and moving horizontally with velocity 2omegaR towards centre of the disc collides and sticks to its rim. The impulse on the particle due to the disc is
05:09View SolutionA uniform rod of mass 200 grams and length L = 1m is initially at rest in vertical position. The rod is hinged at centre such that it can rotate freely without friction about a fixed horizontal axis passing through its centre. Two particles of mass m = 100 grams each having horizontal velocity of equal magnitude u = 6 m/s strike the rod at top and bottom simultaneously as shown and stick to the rod. Find the angular speed (in rad/sec.) of rod when it becomes horizontal.
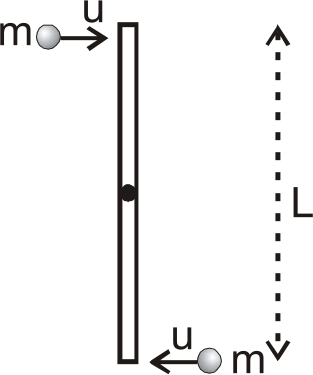03:54View SolutionAn uniform rod of mass m=30kg and length l=0.80m is free to rotate about a horizontal axis O passing through its centre. A particle P of mass M=11.2kg falls vertically through a height h=36245m and collides elastically with the rod at a distance l4 from O. at the instant of collision the rod was stationary and was at angle α=37∘ with horizontal as shown in figure
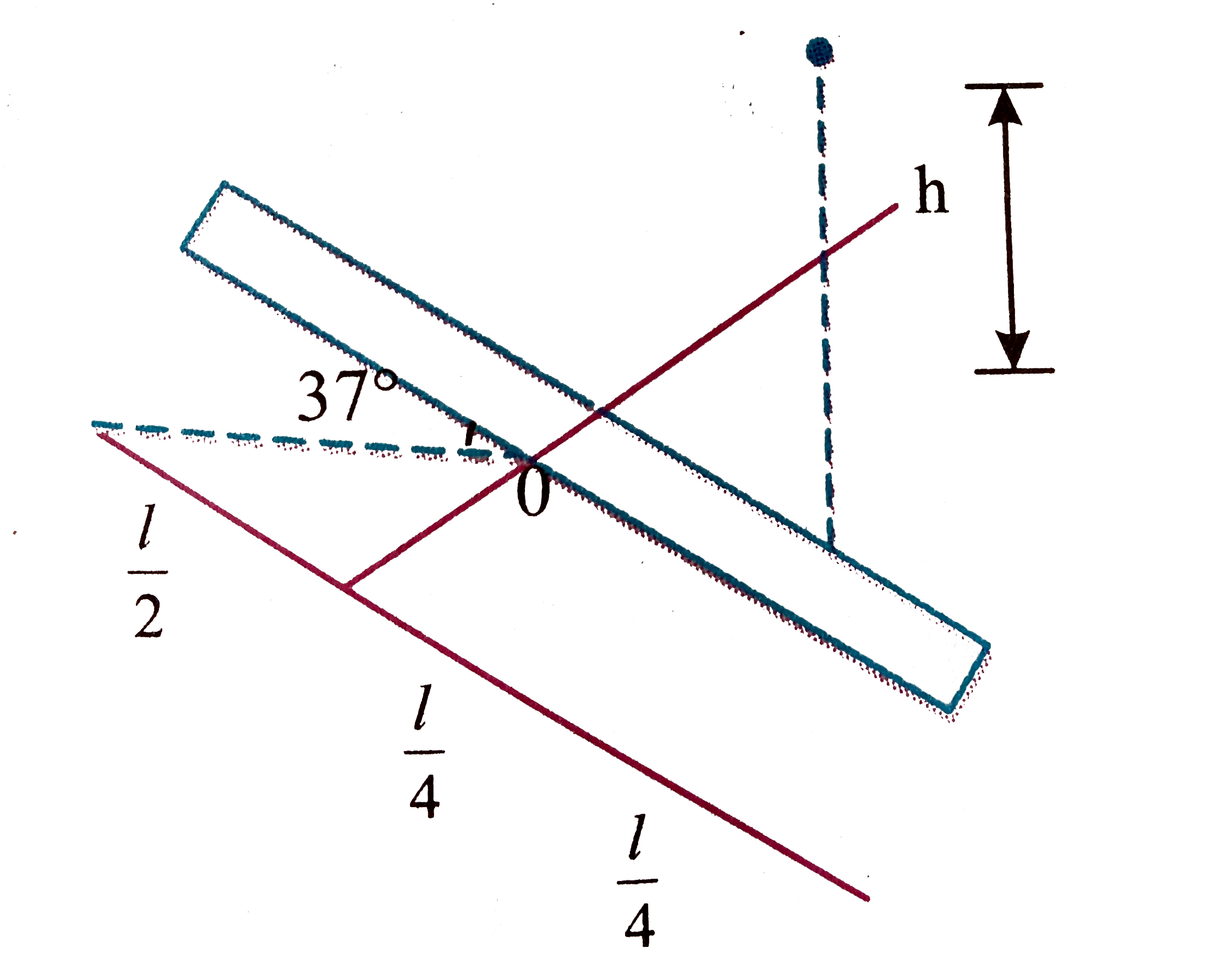
Velocity of particle P after collision (g=10ms−2)View SolutionIn the figure shown, the cart of mass 6m is initially at rest. A particle of mass m is attached to the end of the light rod which can rotate freely about A. If the rod is released from rest in a horizontal position shown, determine the velocity vrel of the particle with respect to the cart when the rod is vertical. (Assume frictionless surface)
04:23View SolutionL लबाई की नगण्य भार वाली क्षैतिज छड़ के दोनों सिरों पर m द्रव्यमान बाली दो छोटी गेदे दृढ़तापूर्वक जोड़ी गई है। छड़ अपने केंद्र से गुजरनेवाले ऊर्ध्वाधर अक्ष के परितः स्वतंत्र रूप से घूम सकती है। निकाय को अक्ष के परितः ω कोणीय चाल से घुमाया जाता है। स्थिर अवस्था में रखा हुआ द्रव्यमान का एक कण P एक गेंद से टकरा जाता है और उसमें चिपक जाता है। छड़ की नई कोणीय चाल ज्ञात करे
View SolutionL लबाई की एक एकसमान छड़ के दानों किनारों पर 1 द्रव्यमान की गेंद लगी है। यह छड़ अपने मध्यबिंदु से जाते लंबवत अक्ष के परित स्वतंत्र रूप से घूम सकती है। यह अक्ष क्षैतिज अवरथा में रहता है। प्रारंभ में निकाय को क्षैतिज अवस्था में रखा गया है। गैंद B पर h ऊँचाई से समान द्रव्यमान n का एक कण P गिराया जाता है। कण गेंद B से टकराकर चिपक जाता है
(a) टक्कर के तुरंत बाद निकाय का कोणीय संवेग तथा कोणीय चाल ज्ञात करें।
(b) h का न्यूनतम मान कितना होना चाहिए ताकि टक्कर के बाद निकाय एक पूरा चक्कर लगा पाए04:23View SolutionOne end of a uniform rod of mass m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity ω. The force exerted by the clamp on the rod has a horizontal component.
View SolutionOne end of a uniform rod of mass m and length / is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity ω. The force exerted by the clamp on the rod has a horizontal component.
View SolutionOne end of a uniform rod of mass m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity ω. The force exerted by the clamp on the rod has a horizontal component.
05:22View Solution