The block of mass m1 shown in figure is fastened to the spring and the block of mass m2 is placed as against it. Find the compression of the spring in the equilibrium position.
 Solution in Tamil
Solution in Tamil
The correct Answer is:→x=(m1+m2)gsinθk
x1=2k(m1+m2)gsinθ
v=√{3k(m1+m2)}gsinθ
a. At the equilibrium condition
kx=(m1+m2)gsinθ
→x=(m1+m2)gsinθk
b. x1=2k(m1+m2)gsinθ
given When the system is released it will start to make SHM.
where , ω=√km1+m2
when the blocks lose contact
p=0
So m2gsinθ=m2x2×km1+m2
→x2=(m1+m2)gsinθk
so the blocks will lose contact with each other when the springs attain its natural length.
c.Let the common speed attained you both the block be v
12(m1+m2)v2−0
=11k(x1+x2)2−(m1+m2)gsinθ(x+x1)
[x+x1=total compression]
→12(m1+m2)v2
=12k(3k)(m1+m2)gsinθ−(m1+m2)gsinθ−(x1+x2)
→12(m1_m2)v2=
12(m1+m2)gsinθ×(3k)(m1+m2)gsinθ<br>rarr v=√{3k(m1+m2)}gsinθ
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-216videos
SIMPLE HARMONIC MOTION
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises86videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises32videos
SOME MECHANICAL PROPERTIES OF MATTER
Similar Questions
Select the correct statements
10:42View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration.
09:46View SolutionA load of 10 kg is suspended by a metal wire 3 m long and having a cross sectional area 4mm2. Find a. the stress b. the strain and c. the elongation. Young modulus of the metal is2.0×1011Nm−2
07:12View SolutionThe block of mass m1 shown in figure is fastened to the spring and the block of mass m2 is placed asgainst ilt. A. Find the compression of the spring in the equilibrium position. b.The blocks are pushed a further distance (2k)(m1+m2)gsinθ against the spring and released. Find the position where the two blocks separate. c. What is the common speed of blocks at the time of separation?
 08:46View Solution
08:46View SolutionA block of mass m is released from rest onto a spring. A having stiffness kA=mg/2h as shown in figure. If the block compresses spring B through a distance h, find the:

a. stiffness of the spring B
b. equilibrium position of the block
c. maximum velocity of the block
d. maximum acceleration of the block02:01View Solution
Two blocks are placed at rest on a smooth fixed inclined place. A force F acts on block of mass m1 and is parallel to the inclined plane as shown in figure. Both blocks move up the incline. Then
(i) Draw free body diagram blocks of mass m1 and blocks mass m2
(ii) Find acceleration of blocks of mass m1 and blocks mass m2
(iii) Find normal reaction between the blocks of mass m1 and m203:20View SolutionA block of mass m moving at a speed v_0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
06:01View SolutionTwo springs are in a series combination and are attached to a block of mass 'm' which is in equilibrium. The spring constants and extension in the springs are as shown in the figure. Then the force exerted by the spring on the block is :
 01:51View Solution
01:51View SolutionA block of mass m compresses a spring iof stifffness k through a distacne l//2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
06:42View SolutionA block of mass m is placed on a smooth block of mass M = m with the help of a spring as shown in the figure. A velocity v_(0) is given to upper block when spring is in natural length. Find maximum compression in the spring.
View SolutionSpring of spring constant k is attached with a block of mass m_(1) , as shown in figure. Another block of mass m_(2) is placed angainst m_(1) , and both mass masses lie on smooth incline plane. Find the compression in the spring when lthe system is in equilibrium.
13:52View SolutionTwo blocks of masses m1andm2 are connected by a spring of spring constant k figure. The block of mass m2 is given a shape impulse so that it acquires a velocity v0 towards right. Find a. the velocity of the centre of mass b. the maximum elongation that the spring will suffer.
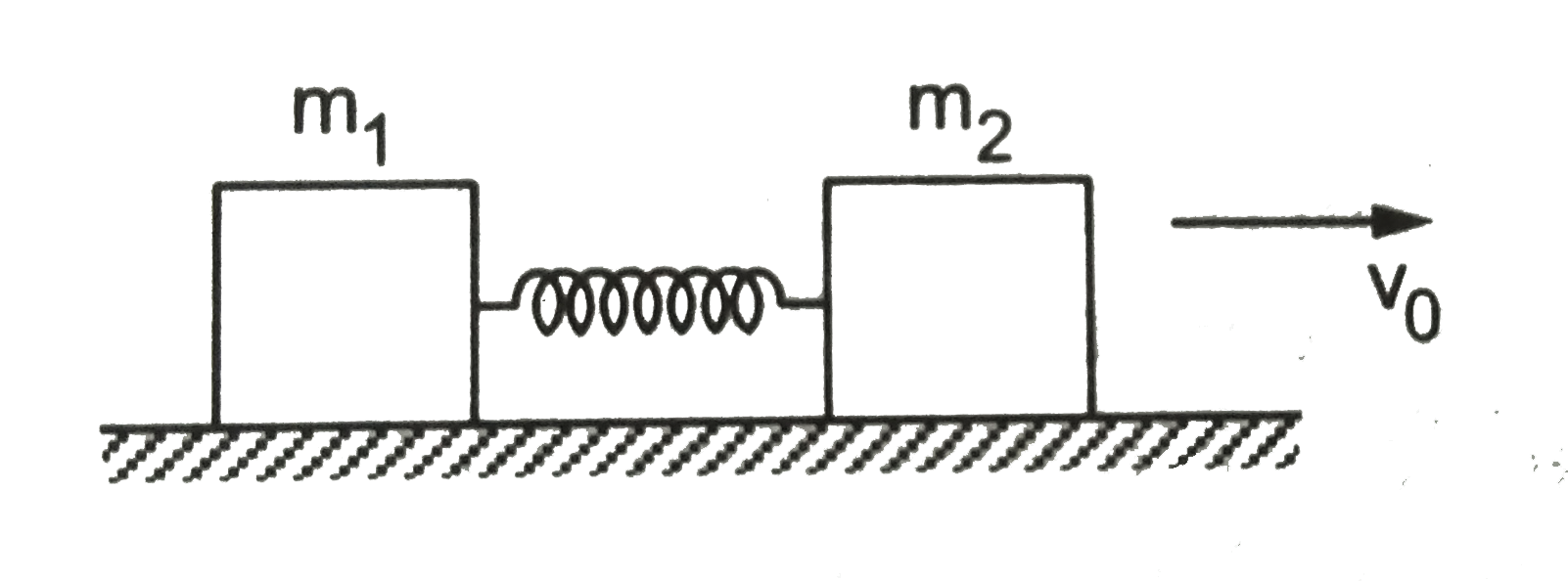 05:07View Solution
05:07View SolutionThe block of mass m_1 shown in figure is fastened to the spring and the block of mass m_2 is placed against it. (a) Find the compression of the spring in the equilibrium position. (b) The blocks are pushed a further distance (2/k) (m_1 + m_2) g sin theta against the spring and released. Find the position where the two blocks seperate (c) What is the common speed of blocks at the time of separation ?
01:53View SolutionA block of mass m is released from rest onto a spring. A having stiffness kA=mg/2h as shown in figure. If the block compresses spring B through a distance h, find the:

a. stiffness of the spring B
b. equilibrium position of the block
c. maximum velocity of the block
d. maximum acceleration of the block05:24View Solution
Two blocks are placed at rest on a smooth fixed inclined place. A force F acts on block of mass m1 and is parallel to the inclined plane as shown in figure. Both blocks move up the incline. Then
(i) Draw free body diagram blocks of mass m1 and blocks mass m2
(ii) Find acceleration of blocks of mass m1 and blocks mass m2
(iii) Find normal reaction between the blocks of mass m1 and m202:35View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :02:35View Solution

