Two blocks of masses 1 kg and 2kg are connect by a metal wire going over a smooth pulley as shown in figure. The breaking stress of the metal is 2×109Nm−2. What should be the minimum radius of the wire used if it is not to break? Take g=10ms−2
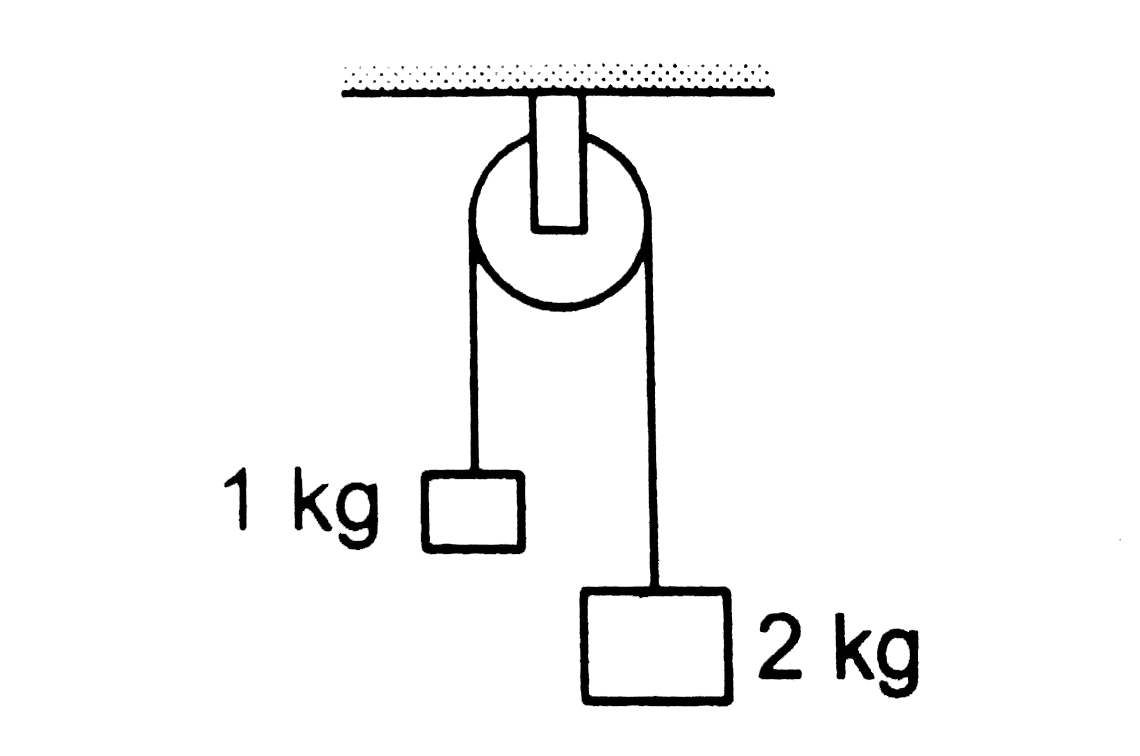 Solution in Tamil
Solution in Tamil
The stress in the wire =TensionAreaofcrosssection
To avoid breaking, this stress should not exceed the breaking stress.
Let the tension in the wire be T. The equations of motion of the two blocks are
T−10N=(1kg)a
and20N−T=(2kg)a
ElimiN/Ating a from these equations
T=(403)N
Thestress=(403)Nπr2
If the minimum radius needed to avoid breaking is r, 2×109Nm2=(403)Nπr2
solv∈gthis<br>r=4.6xx10^-5m.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Question For short Anser18videos
SOME MECHANICAL PROPERTIES OF MATTER
- BOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-129videos
SOME MECHANICAL PROPERTIES OF MATTER
- BOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises32videos
SOME MECHANICAL PROPERTIES OF MATTER
- BOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises58videos
SIMPLE HARMONIC MOTION
- BOOK - HC VERMACHAPTER - SOUND WAVESEXERCISE - All Questions139videos
SOUND WAVES
Similar Questions
The ratio stress/strain remains constant for small deformation of a metal wire. When the deformation is made larger, will this ratio increase or decrease ?
04:48View SolutionA rope 1 cm in diameter breaks if the tension in it exceeds 500 N. The maximum tension that may be given to a similar rope of diameter 2 cm is
02:19View SolutionA load of 10 kg is suspended by a metal wire 3 m long and having a cross sectional area 4mm2. Find a. the stress b. the strain and c. the elongation. Young modulus of the metal is2.0×1011Nm−2
03:46View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
06:02View SolutionA wave of wavelength 0.60 cm is produced in air and it travels at a speed of 300 ms^-1. Will it be audible?
04:05View SolutionTwo blocks of masses 1 kg and 2 kg are connected by a metal wire goijng over a smooth pulley as shown in figure. The breaking stress of the metal is (40//3pi)xx10^(6)N//m^(2) . If g=10ms^(-12) , then what should be the minimum radlus of the wire used if it is not to break?
03:37View SolutionTwo blocks of masses m and 2m are connected through a wire fo breakig stress S passing over a frictionless pulley. The maximum radius of the wire to be used so that the wire may not break is
04:05View SolutionTwo blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2×109Nm−2. What would be the minimum radius of the wire used if it not to break ? Take ,g=10ms−2
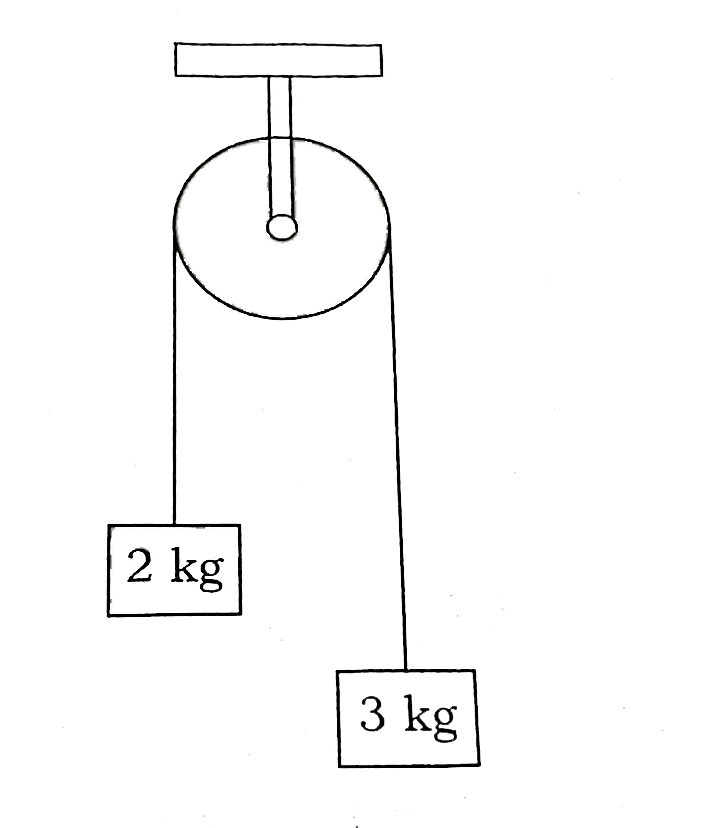 02:54View Solution
02:54View Solutionचित्र 26. W1 में एक चिकनी घिरनी दिखाई गई है जिसपर से एक धातु का तार जा रहा है। तार के सिरों पर 1 kg तथा 2 kg के द्रव्यमान बँधे है। इस धातु का breaking stress 2×109N/m2 है। इस तार की न्यूनतम त्रिज्या कितनी हो सकती है कि तार न टूटे? g का मान 10m/s2 लें तथा तार के भार को नगण्य मानें।
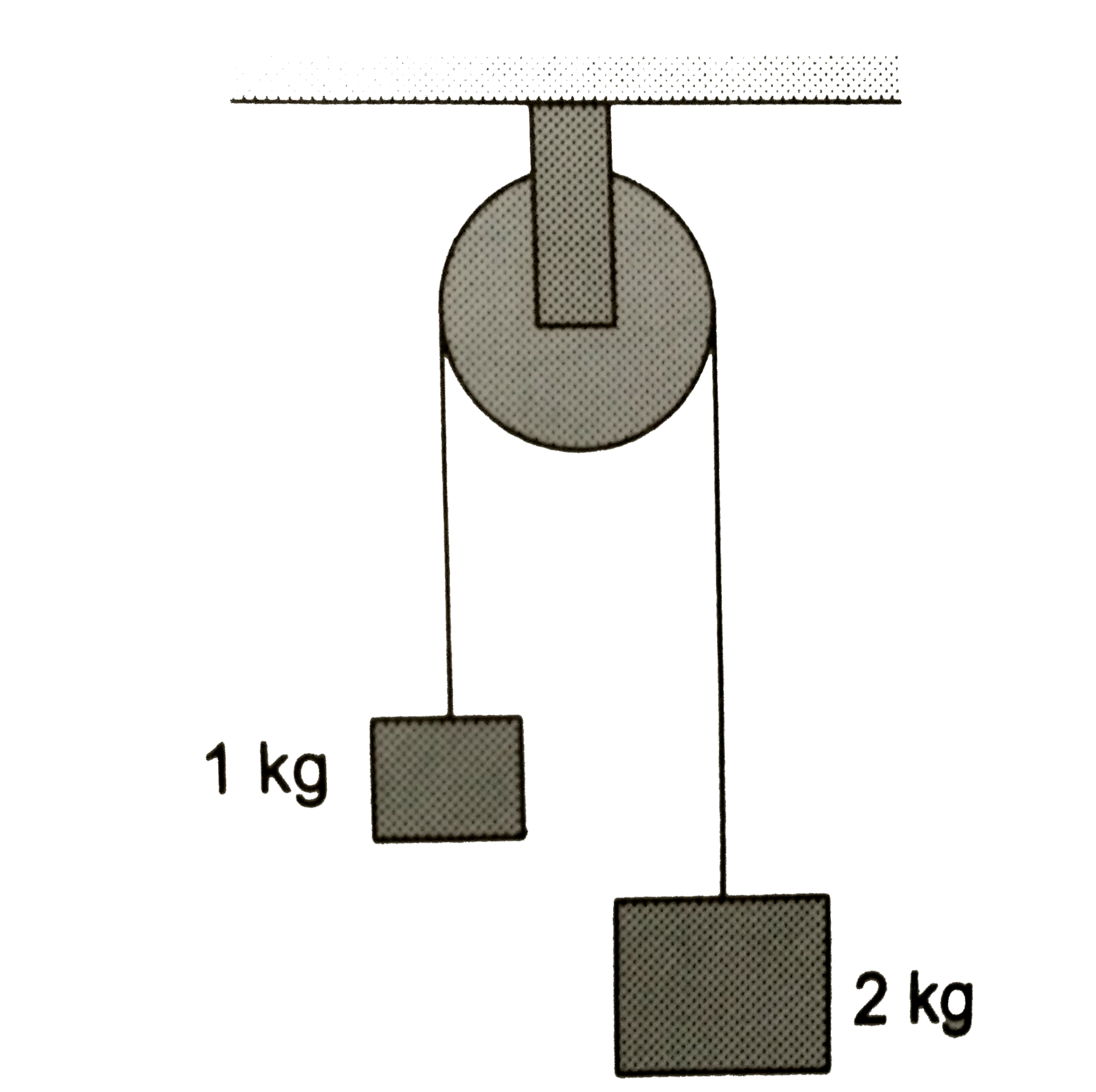 04:05View Solution
04:05View SolutionTwo block of masses 1 kg 2 are connected by a metal wire going over a smooth pulley. The breaking stress of metal is 40/(3pi) xx10^(6)Mm^(-2) . What should be the minimum radius of wire used if it should not break? (g=10ms^-2)
03:50View SolutionTwo blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2xx10^(9)"N m"^(-2) . If g=10ms^(-2) , then what is the minimum radius of the wire which will not break
03:18View SolutionTwo block of masses 1 kg 2 are connected by a metal wire going over a smooth pulley. The breaking stress of metal is 403π×106Mm−2 . What should be the minimum radius of wire used if it should not break?(g=10ms−2)
03:50View SolutionTwo blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?
 02:42View Solution
02:42View SolutionTwo block of masses 1 kg 2 are connected by a metal wire going over a smooth pulley. The breaking stress of metal is 403π×106Mm−2 . What should be the minimum radius of wire used if it should not break?(g=10ms−2)
06:32View SolutionTwo blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2xx10^(9)Nm^(-2) . What would be the minimum radius of the wire used if it not to break ? Take , g=10 ms^(-2)
03:27View SolutionTwo blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?
 03:49View Solution
03:49View Solution
