The length of the wire shown in figure between the pulley is 1.5 m and its mass is 12.0 g. Find the frequency of vibration with which the wire vibrates in two loops leaving the middle point of the wire between the pulleys at rest.
Solution in Tamil
The correct Answer is:70Hz
L=1.5m,mass=12gm
Mass per unit length
m=1215gm
=8×10−3kgm
T=9×g
=90N,λ=1.5m
f1=22L√(Tm)
[for second harmonic two loops are produced]
f1=2f0=11.5√(908×10−3)
=(1.6.06)1.5
=70.7Hz≈70Hz
Topper's Solved these Questions
Similar Questions
A mechanical wave propagastes in a medium along the X-axis. The particles of the medium moves in what direction?
01:58View SolutionThe gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67×10−17N. Calculate the separation between the particles.
01:44View SolutionThe mass of a cyclist together with the bicycle is 90 kg. Calculate the work done by cyclist if the speed increases from 6km/h to 12 km/h.
03:16View Solution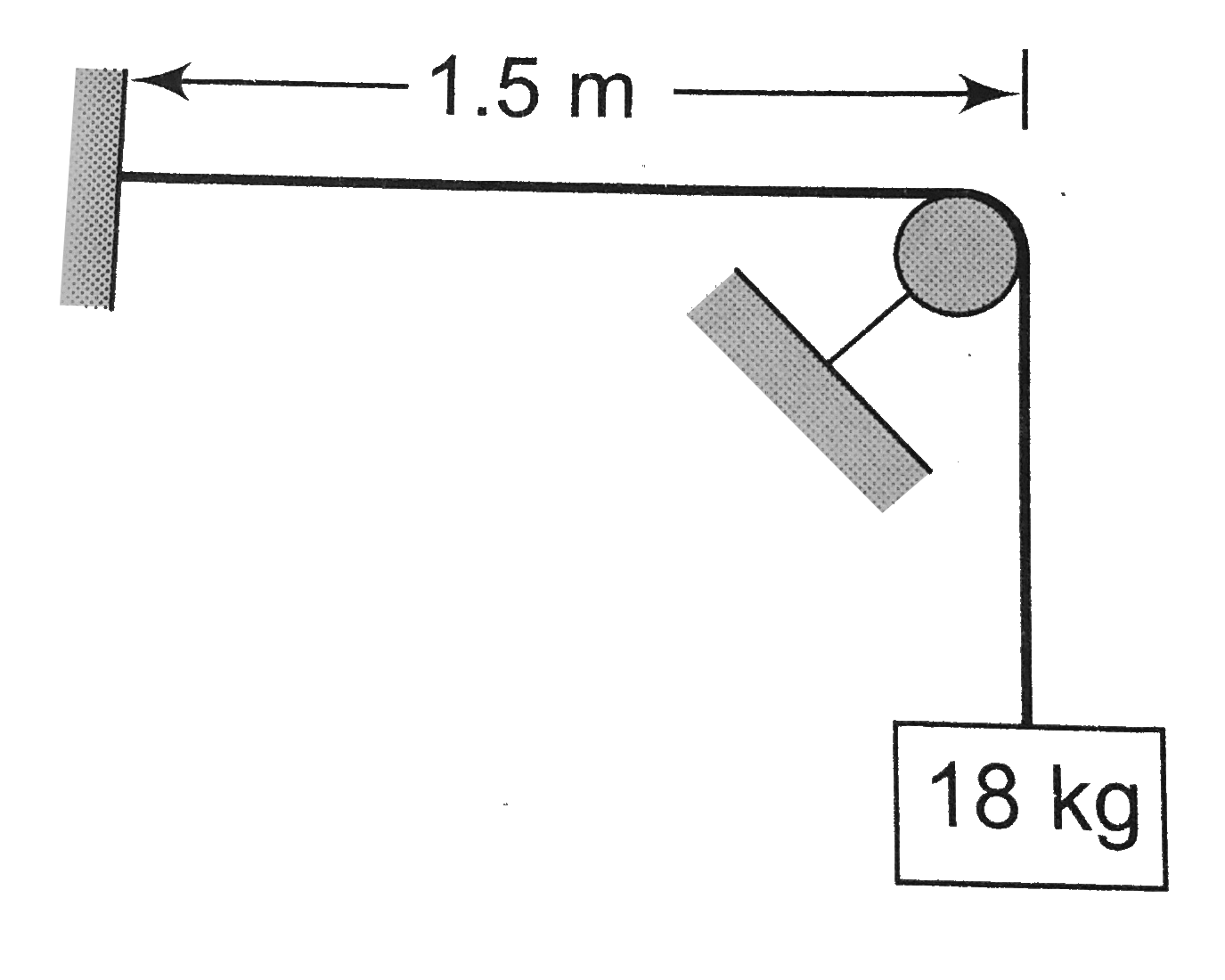
The length of the wire shown in Fig. Between the pulley and fixed support is 1.5m and mass is 12.0g the frequency of vibration with which the wire vibrate two loops leaving the middle point of the wire between the pulleys at rest is01:44View SolutionThe length of the wire shown in figure between the pulleys is 1.5 m and its mass is 15 g. what is the frequency of vibration with which the wire vibrates in four loops leaving the middle point of the wire between the pullys at rest ? (g=10ms2)
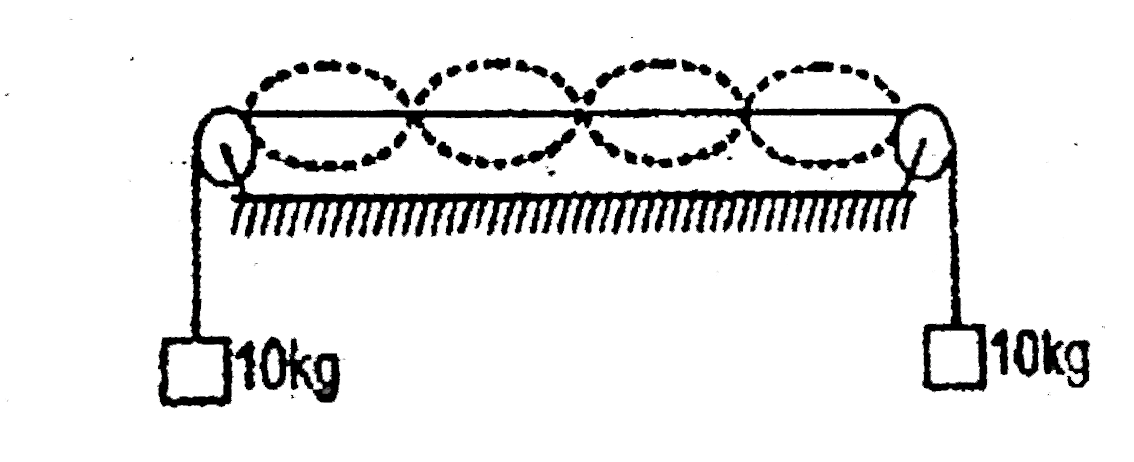02:26View SolutionThe length of the wire shown in the figure between the pulleys is 1.5m and its mass is 12.0g. The frequency of vibration with which the wire vibrates in three loops forming antinode at the mid point of the wire is - (Take g=9.8 m//s^2 )
02:15View SolutionA 50cm long wire of mass 20g supports a mass of 1.6kg as shown in figure. Find the first overtone frequency of the portion of the string between the wall and the pulley. Take g=10m/s2
02:36View SolutionFrequency of vibration of a wire varies inversely with its length. The frequency is 220 Hz when the length of the wire is 120m. Find the frequency of the wire when its length is 100 m.
05:10View Solutionएक तने हुए तार की लम्बाई 1.0 मीटर तथा द्रव्यमान 0.2 ग्राम है । यदि तार से 2.5 किग्रा का भार लटक रहा हो और तार दो खण्डों में कम्पन कर रहा हो तो तार में उत्पन्न स्वर की आवृत्ति ज्ञात कीजिये । (g=10मीटर/सेकण्ड2)
04:50View Solutionएक सोनोमीटर का तार 256 Hz आवृत्ति वाले स्वरित्र द्विभुजके साथ अनुनाद में है। सेतुओं के बीच तार की लंबाई 1.5 m है तथा यह तार दो लूपों में कम्पन करता है । इस तार पर यदि अनुप्रस्थ तरंगिका भेजी जाए, तो इसकी चाल कितनी होगी ?
03:36View Solutionचित्र में दिखाई गई घिरनियों के बीच तार की लंबाई 1.5m है तथा इसका द्रव्यमान 12.0g है। यदि इस तार को दो लूपों में कंपित कराया जाए, तो उसकी कंपन आवृत्ति क्या होगी ।
05:58View Solutionएक सितार का तार 330 कम्पन/सेकण्ड की आवृत्ति से कम्पन करता है । यदि तार की लम्बाई तीन गुनी तथा खिचाव बल चार गुना कर दिया जाए, तो उसकी आवृत्ति क्या होगी ?
05:05View SolutionIn a sonometer wire, the tension is maintained by suspending a 20kg mass from the free end of the wire. The fundamental frequency of vibration is 300Hz . If the tension is provided by two masses of 6kg and 14kg suspended from a pulley as show in the figure the fundamental frequency will
04:41View SolutionThe figure shows two creates that are connected by a steel wire that passes over a pulley. The unstretched length of the wire is 1.5 m, and its cross - sectional area is 1.3xx10^(-5)m^(2) . The pulley is frictionless and massless. When the crates are accelerating, determine the change in length of the wire. Ignore the mass of the wire.
04:41View SolutionA wire when stretched between two rigid supports under a tension of 60 N vibrates in p loops. The frquency at which the wire resonates is 318 Hz and the next frequency when it resonates is 390 Hz. Find the values of p and length of wire if mass per unit length of the wire is 10^(-4) kg/m.
02:59View SolutionThe length of wire between the pulleys displayed in the picture is 1.5 m and its mass is 12.0 grams. The wire between the two pulleys is vibrating in three loops, making the vibrations at the center, the vibrations of the vibrations. (g = 9.8 m//s^(2))
03:46View Solution