Two identical particles each of mass m and charges -q and + q are revolving around their common centre of mass, in a circle of radius r, under the influence of electrostatic attraction. The kinetic energy of each particle is .
q24πε0(4r)
14πε0q2(2r)
14πε0q28r
14πε0q2r
The correct Answer is:A

∴q24πε0(2r)2=μv22r …(1)
where μ = reduced mass of syetem
=m1m2m1+m2
∴ m1=m2=m
∴ μ=m2
from eqn . (1)
∴ K.E=12μv2
=12×14πε0q22r=q24πε0.4r
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - LEVEL -II
74 Videos
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - LEVEL-III
23 Videos
- ELECTRONS & PHOTONSBOOK - MODERN PUBLICATIONCHAPTER - ELECTRONS & PHOTONSEXERCISE - RECENT COMPETITIVE QUESTIONS
20 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Recent Competitive Questions
8 Videos
Similar Questions
Two particles of equal mass (m) move in a circle of radius (r ) under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionTwo particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution
Knowledge Check
Two particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
AV=12R√1GmBV=√GM2RCV=12√GmRDV=√4GmRTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of each particle is
A12R√(1Gm)B√(Gm2R)C12√(GmR)D√(4GmR)Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
A√GMRB√2√2GMRC√GMR(1+2√2)D12√GMR(1+2√2)
Two particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionFour particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
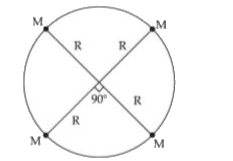
View SolutionTwo particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
View SolutionTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of earth particle is
View SolutionFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
View Solution
