Two positive charges of magnitude 'q' are placed at the ends of a side (side 1 ) of a square of side 2a . Two negative charges of the same magnitude are kept at the other corners . Starting from rest , if a charge Q moves from the middle of side 1 to the centre of square , its kinetic energy at the centre of square is :
zero
14πε02qQa(1+1√5)
14πε02qQa(1−1√5)
14πε02qQa(1−1√5)
The correct Answer is:D
Work done on charge Q = change in K.E = Ef−Ef=Ef−0
∴Q(VA−VB)=Ef
Q(24πε0qa−24πε0q√5a−0)=Ef
∴E6=2qQ4πε0a(1−1√5)
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - RECENT COMPETITIVE QUESTIONS
39 Videos
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - LEVEL -II
74 Videos
- ELECTRONS & PHOTONSBOOK - MODERN PUBLICATIONCHAPTER - ELECTRONS & PHOTONSEXERCISE - RECENT COMPETITIVE QUESTIONS
20 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Recent Competitive Questions
8 Videos
Similar Questions
Two positive charges of magnitude q are placed at the ends of a side ( side 1) of a square of side 2a . Two negative charges of the same magnitude are kept at the other corners . Staring from rest , a charge Q moves from the middle of side 1 to the centre of square , its kinetic energy at the centre of square is -.
View SolutionThree positive charges of equal magnitude q are placed at the vertics of and equilatral triangle of side l. How can the system of charges be palced in equilibrium?
View Solution
Knowledge Check
Two positive charges of magnitude q are placed at the ends of a side ( side 1) of a square of side 2a . Two negative charges of the same magnitude are kept at the other corners . Staring from rest , n a charge Q moves from the middle of side 1 to the centre of square , its kinetic energy at the centre of square is -.
A14π∈02qQa(1+1√5)B14π∈02qQa(1+1√5)C14π∈02qQa(1+1√5)D14π∈02qQa(1+1√5)Two positive charges of magnitude q are placed at the ends of a side (side 1 ) of square of side 2a. Two negative cahrges of the same magnitude ar kept at the other comers. Starting from rest, if the charge Q moves from the middle of side (1) to the centre of square , its kinetc energy at the centre of square is
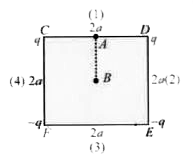 A14π∈02qQa(1−1√5)BzeroC14π∈02qQa(1+1√5D14π∈02qQa(1−2√5)
A14π∈02qQa(1−1√5)BzeroC14π∈02qQa(1+1√5D14π∈02qQa(1−2√5)Three positive charges of equal magnitude q are placed at the vertices of and equilateral triangle of side l. How can the system of charges be placed in equilibrium?
Aby placing a charge Q=−q/√3 at the centroid of the triangleBby placing a charge Q=q/√3 at the centroid of the triangleCby placing a charge Q=q at the centroid of the triangleDby placing a charge Q=−q at the centroid of the triangle
Four charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionFour charges of same magnitude and same sign are placed at the corners of a square, of each side0⋅1m. What is electric field intensity at the center of the square?
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View Solution
