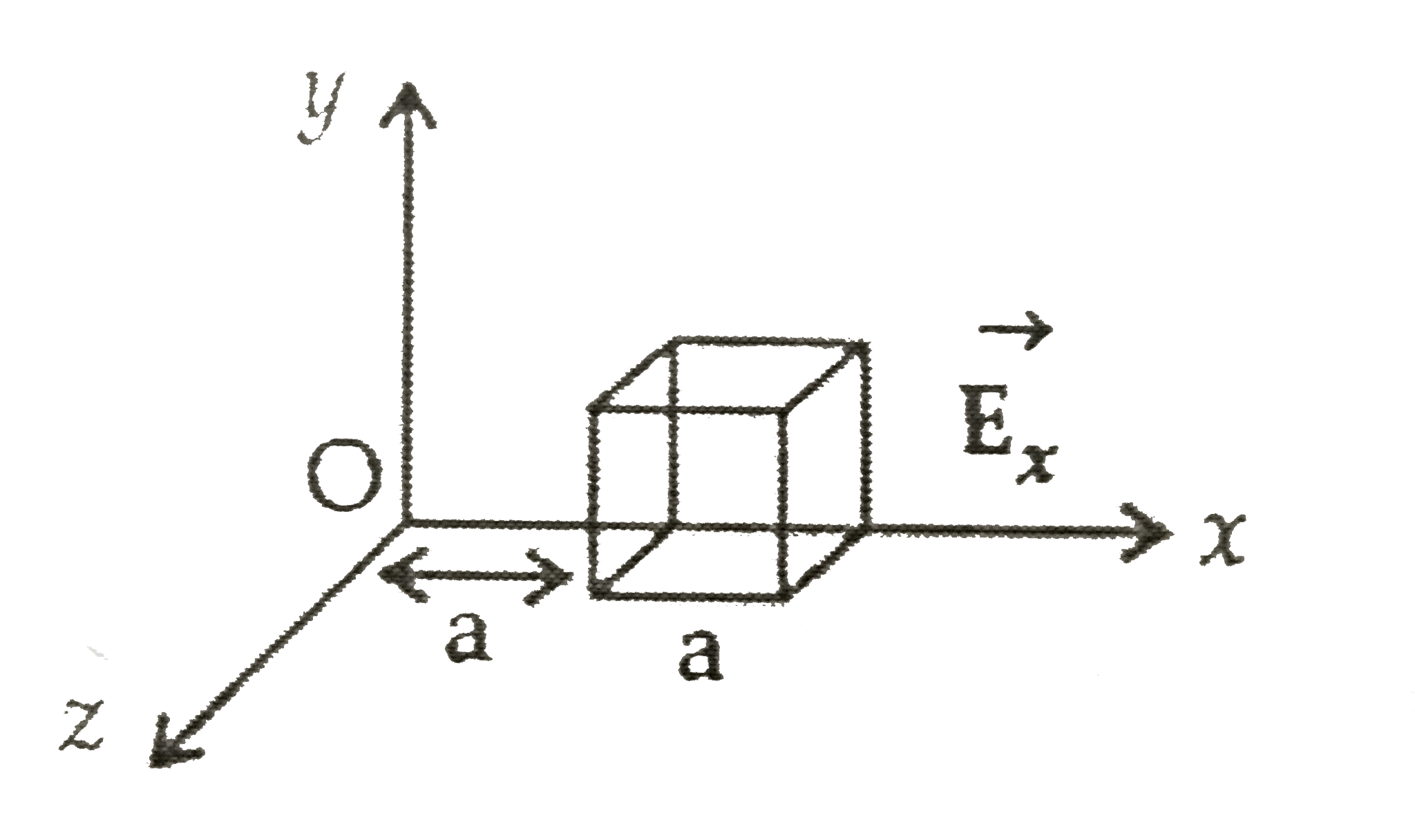
The electric field component in Fig. , are Ex=αx1/2,Ey=Ez=0 in whichα=800 N/C m1/2 Calculate the flux through the cube, and Assume that A= 0.1 M

1.05Nm2C−1
10.5Nm2C−1
105Nm2C−1
Zero
The correct Answer is:A
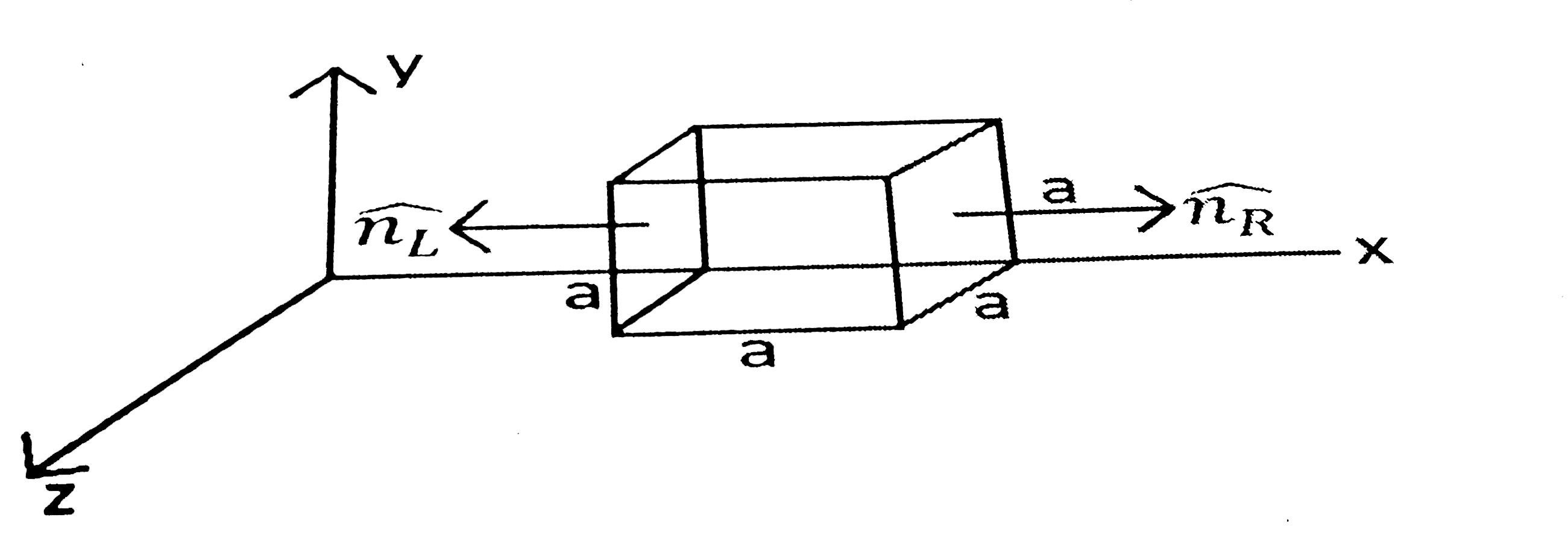
Given : Ey=Ex=0,
Ex=αx1/2
α=800N/Cm1/2
a = 0.1 m
Here , electric field has only x component .
At the left face , x = a .
So , magnitude of the electric field on this face is
Eleft=αa1/2
At the right face m x = 2a
So magnitude of the electric field on this face is
Enight=α(2)1/2=√2αa1/2
As both the electric fields , →Eleftand→Eright , are directed in opposite directions to each other , i.e towards ˆnLandˆnR , therefore net flux through the cube is given as
ϕ=ϕ right−ϕleft
or ϕ=(Eright) (area of the right face ) - (Eleft) (area of the left face )
or ϕ=(√2αa1/2(a2)−(αa1/2)(a2)
or ϕ=α5/2(√2−1)
=(800N/Cm1/2)(0.1)5/2(√2−1)
This gives ϕ=1.05 N m2C−1 .
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - LEVEL -II
74 Videos
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - LEVEL-III
23 Videos
- ELECTRONS & PHOTONSBOOK - MODERN PUBLICATIONCHAPTER - ELECTRONS & PHOTONSEXERCISE - RECENT COMPETITIVE QUESTIONS
20 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Recent Competitive Questions
8 Videos
Similar Questions
Using Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
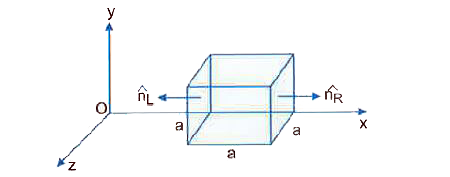
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
View SolutionUsing Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.

View Solution
Knowledge Check
The electric components in the figure are Ex=αx1/2,Ey=0,Ez=0 where α=800N/m2 if a=0.1m is the side of cube then the charge with in the cube is
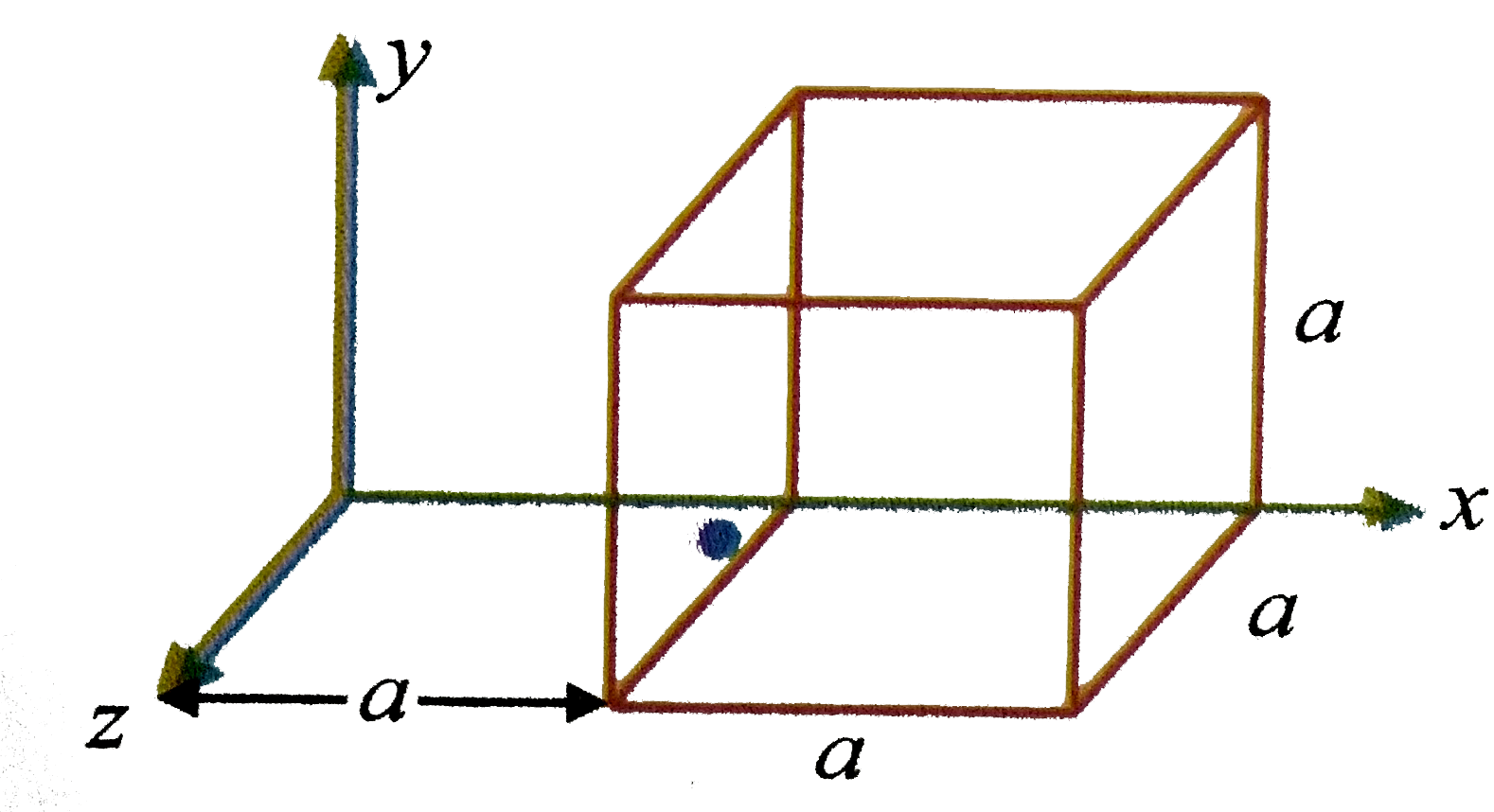 A9.27×10−12CB6×10−12CC2.5×10−12CDZero
A9.27×10−12CB6×10−12CC2.5×10−12CDZero
(a) Using Gauss's law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
(b) The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/Cm. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a=0.1m.
View SolutionDefine electric flux and write its SI unit . The electric field components in the figure shown are : Ex=αx,Ey=0,Ez=0 where α=100NCm.
Calculate the charge within the cube , assuming a = 0.1 m .
View SolutionDefine electric flux and write its SI unit . The electric field components in the figure shown are : Ex=αx,Ey=0,Ez=0 where α=100NCm.
Calculate the charge within the cube , assuming a = 0.1 m .

View SolutionThe electric components in the figure are Ex=αx1/2,Ey=0,Ez=0 where α=800N/m2 if a=0.1m is the side of cube then the charge with in the cube is
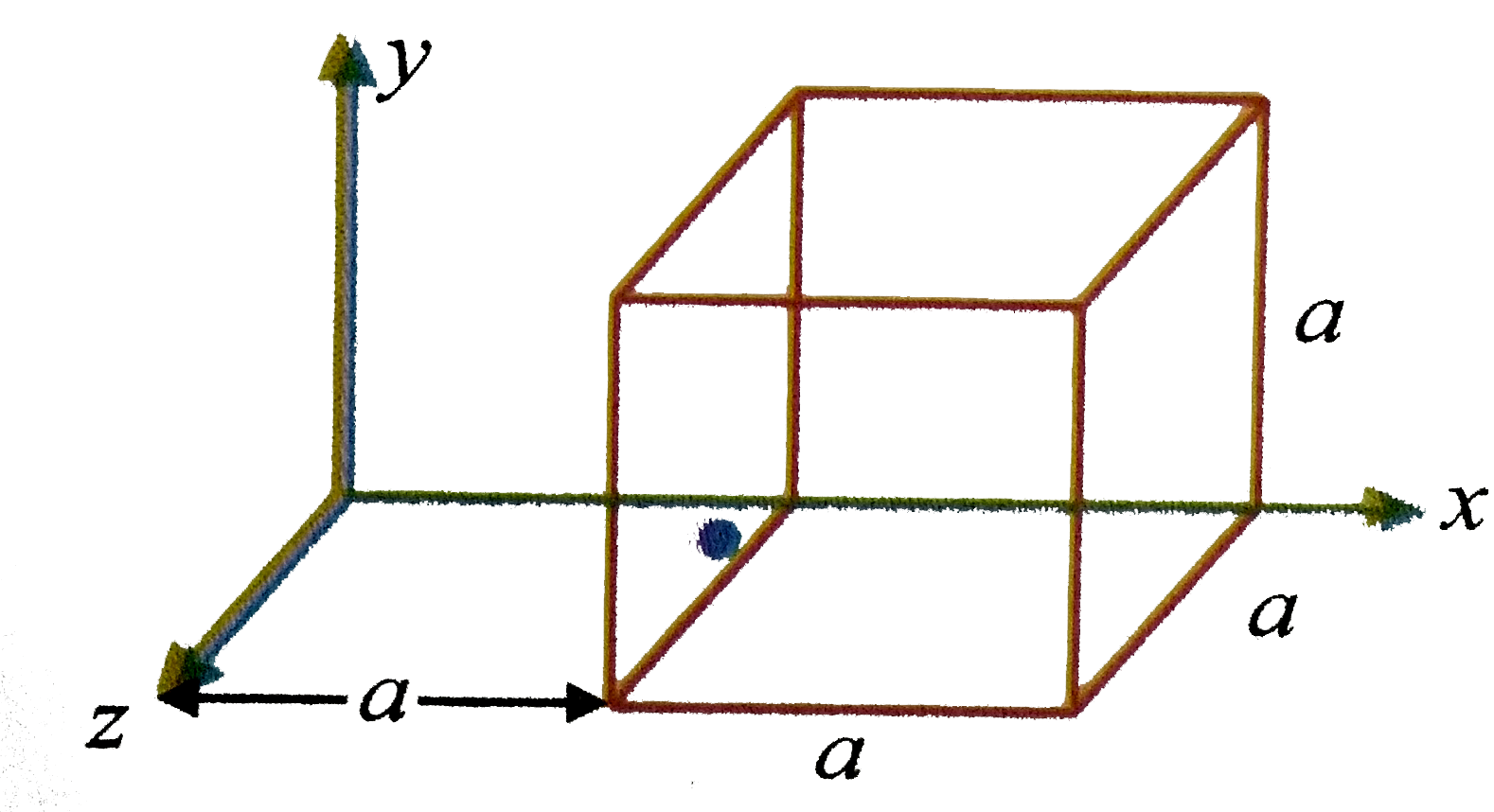
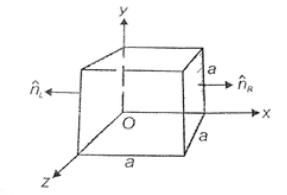
View SolutionThe electric field components in the figure below are Ex=800x2N/C,Ey=Ez=0.
Calculate
(1) The flux throught he cube and
(2) The charge withing the cube
Assume that a =0.1 m
View SolutionThe electric field componets due to a charge inside the cube of side 0.1m are Ex=αx, where α=500(N/C)m−1,
Ey=0,Ez=0. Calculate the flux through the cube and the charge inside the cube.
View Solution(a) Define electric flux. Write its SI units.
(b) The electric field components due to a charge inside the cube of side 0.1 m are as shown :
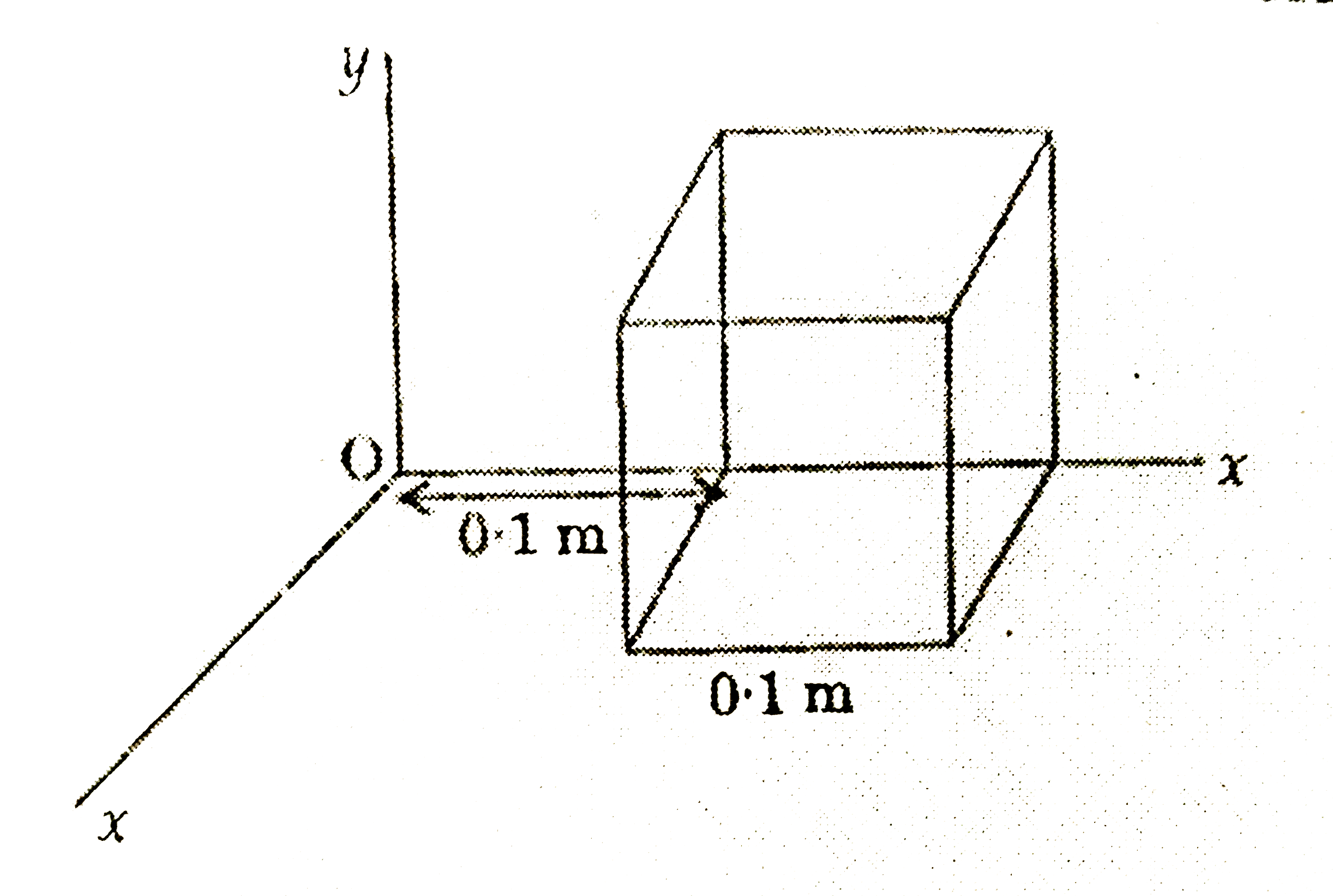
Ex=αx, where α=500N/C−m
Ey=0,Ez=0.
Calculate (i) the flux through the cube, and (ii) the charge inside the cube.
View Solution
