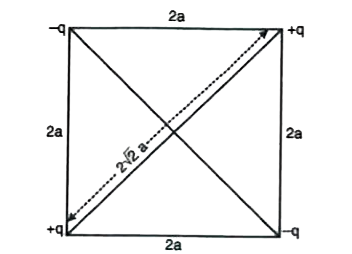
Two identical positive charges are placed at the diagonally opposite corners of a square . Two more identical but negative charges are placed at the other two corners. What is the work done in putting all the charges together at the centre . If q is the magnitude of each charge and 2a is the length of each of the square ?

A

$\frac{\sqrt{2} q^{2}}{8 π ε_{0} a}$

B

$\frac{4 + q^{2}}{8 π ε_{0} a}$

C

$\frac{q^{2} (4 - \sqrt{2})}{8 π ε_{0} a}$

D

$\frac{q^{2} (2 - \sqrt{2})}{8 π ε_{0} a}$

Text Solution

Verified by Experts

The correct Answer is:C

$W = U_{2} - U_{1}, U_{2} = 0$ is P.E at centre
$U_{1}$ = P.E of all in original state

Now
$U_{1} = [\frac{1}{4 π ε_{0}} - \frac{q^{2}}{2 a} - \frac{q^{2}}{2 a} - \frac{q^{2}}{2 a} + \frac{q^{2}}{2 a} + \frac{q^{2}}{\sqrt{2.2 a}} + \frac{q^{2}}{2 \sqrt{2 . a}}]$
$= \frac{- q^{2} . (4 - \sqrt{2})}{8 π ε_{0} a}$
$∴ W = U_{2} - U_{1} = \frac{q^{2} (4 - \sqrt{2})}{8 π ε_{0} a}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
At each corner of an equilateral triangle identical charges are placed. Then at the centre of the triangle
Athe resultant electric intensity is zero
Bthe net potential is zero
Cboth electric intensity and potential are zero
Dneither electric intensity nor potential are zero
Question 2 - Select One
A charges Q is placed at each of the two opposite corners of a square. A charge q is placed to each of the other two corners. If the resultant force on each charge q is zero, then
A $q = \sqrt{2} Q$
B $q = - \sqrt{2} Q$
C $q = 2 \sqrt{2} Q$
D $q = - 2 \sqrt{2} Q$

MODERN PUBLICATION-ELECTROSTATICS-LEVEL -II

Home
Ask Doubt
Profile