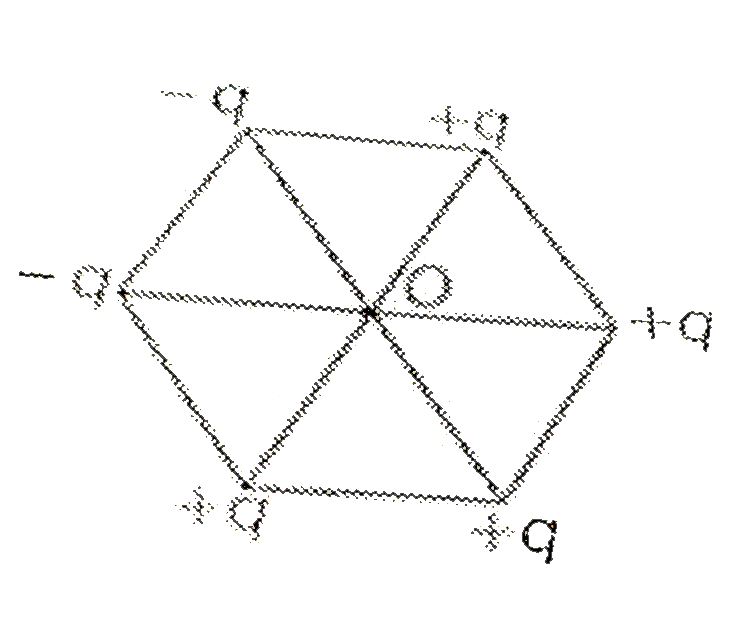
Six point charges are kept at the vertices of a regular hexagon of the side L and centre O , as shown in the figure . Given that K=14πε0qL2 which of the following statement (s) is (are) correct ?
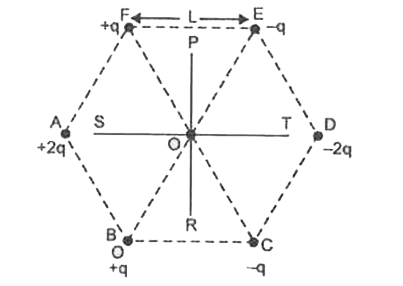
The electric field at O is 6K along OD.
The potential at O is zero .
The potential at all points on the line PR is same .
The potential at all points on the line ST is same .
The correct Answer is:A, B, C
R0=6K (along OD)
V0=0
Pot . On line PR is zero .
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - RECENT COMPETITIVE QUESTIONS
39 Videos
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - LEVEL -II
74 Videos
- ELECTRONS & PHOTONSBOOK - MODERN PUBLICATIONCHAPTER - ELECTRONS & PHOTONSEXERCISE - RECENT COMPETITIVE QUESTIONS
20 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Recent Competitive Questions
8 Videos
Similar Questions
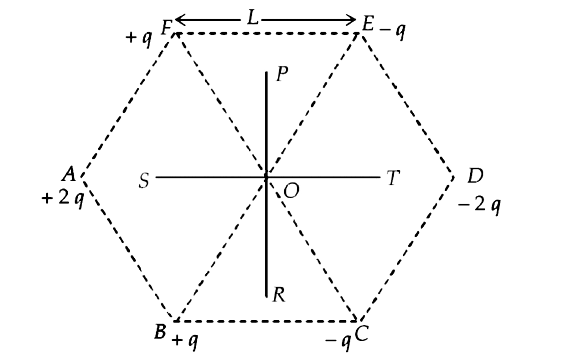
Six point charges are kept at the vertices of a regular hexagon of side L and centre O, as shown in the figure. Given that K=14πε0qL2, which of the following statements(s) is (are) correct?
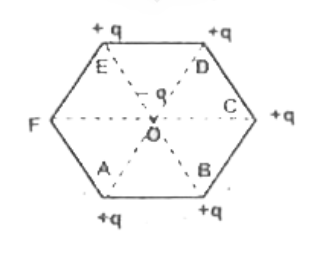
View SolutionFive point charges each of charge +q are placed on five vertices of a regular hexagon of side h as shown in the figure. Then
View Solution
Knowledge Check
Six point charges are kept at the vertices of a regular hexagon of side L and centre O, as shown in the figure. Given that K=14πε0qL2, which of the following statements(s) is (are) correct?
 A(a) The electric field at O is 6K along ODB(b) The potential at O is zeroC(c) The potential at all points on the line PR is sameD(d) The potential at all points on the line ST is same
A(a) The electric field at O is 6K along ODB(b) The potential at O is zeroC(c) The potential at all points on the line PR is sameD(d) The potential at all points on the line ST is sameFive point charges each of charge + q are placed on five vertices of a regular of side h as shown in the figure. Then
Athe forces on (-q) at O due to charges +q at A and D are balanced.Bthe forces on (-q) due to charges at D and E are balanced.CThe resultant force on −q at O is 14πε0q2h2 along OE.DThe resultant force on - q at O is 14πε0q2h2 along OC.Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
AGm2l2[54+1√3]BGm2l2[34+1√3]CGm2l2[54−1√3]DGm2l2[34−1√3]
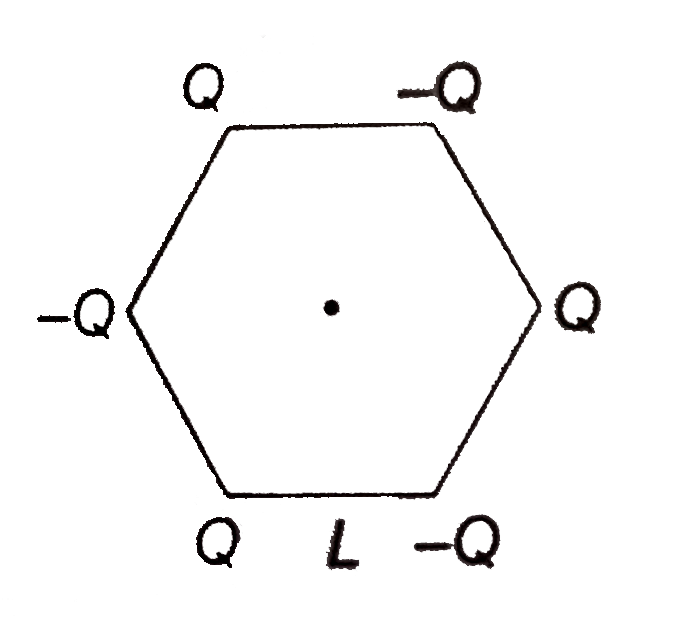
The point charges are placed on the vertices of regular hexagon of side L as shown. Find the potential energy of the system of charges.
View SolutionSix point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
View SolutionSix point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
View SolutionSix point charges are placed at the vertices of a hexagon of side 1 m as shown in figure. Net electric field at the centre of the hexagon is
View SolutionSix point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
Find the magnitude of electric field at the centre of regular hexagon.
View Solution
