A proton (mass m and charge + e) and α - particle (mass 4 m and charge + 2e) are projected with the same kinetic energy at right angles to a uniform magnetic field . Which one of the following statements will true ?
the α particle will be bent in a circular path with smaller radius than proton .
the radius of the path of α - particle will be greater than that of proton.
radius of the paths of both the particles will be the same .
both will go through the magnetic field in the straight line .
The correct Answer is:C
Topper's Solved these Questions
- 15 MAGNETIC EFFECTS OF CURRENTSBOOK - MODERN PUBLICATIONCHAPTER - 15 MAGNETIC EFFECTS OF CURRENTSEXERCISE - Multiple choice questions (Level - I) Paragraph questions
6 Videos
- 15 MAGNETIC EFFECTS OF CURRENTSBOOK - MODERN PUBLICATIONCHAPTER - 15 MAGNETIC EFFECTS OF CURRENTSEXERCISE - Multiple choice questions (Level - I) Assertion and reasoning
44 Videos
- ATOMS, MOLECULES AND NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEIEXERCISE - Recent Competitive Questions
40 Videos
Similar Questions
A proton (mass m and charge +e) and an α-particle (mass 4 m and charge +2e) are projected with the same kinetic energy at right angles to the uniform magnetic field. Which one of the following statements will be true?
View SolutionA proton and an α- particle is projected with equal kinetic energy in transverse uniform magnetic field B. The ratio of radii of proton to that of alpha particle is
View Solution
Knowledge Check
A proton (mass m and charge +e) and an α-particle (mass 4 m and charge +2e) are projected with the same kinetic energy at right angles to the uniform magnetic field. Which one of the following statements will be true?
AThe alpha-particle will be bent in a circular path with a small radius that for the protonBThe radius of the path of the alpha-particle will be greater than that of the protonCThe alpha-particle and the proton will be bent in a circular path with the same radiusDThe alpha-particle and the proton will go through the field in a staight lineStatement-1: A proton and an α- particle are projected with the same kinetic energy at right angles to a uniform magnetic field, then the α-particle will move along a circular path of smaller radius than the proton.
Statement-2: Bqv=mv2rAStatement-1 is true, Statement-2 is true, Statement-2 is a correct explaination of Statement-1.BStatement-1 is true, Statement-2 is true, Statement-2 is not a correct explanation of Statement-1.CStatement-1 is true, Statement-2 is false.DStatement-1 is false, Statement-2 is true.A proton of mass m and charge q is moving in a plane with kinetic energy E. if there exists a uniform magnetic field B, perpendicular to the plane motion. The proton will move in a circular path of radius
A3EmqBB√2EmqBC√Em2qBD√2EqqB
A proton and an alpha particle is projected with equal kinetic energy in transverse uniform magnetic field B. The ratio of radii of proton to that of alpha particle is
View SolutionTwo charged particle M and N are projected with same velocity in a uniform magnetic field. Then M and N respectively.
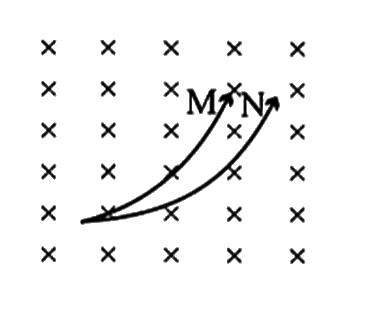
View SolutionTwo charged particle M and N are projected with same velocity in a uniform magnetic field. Then M and N respectively.

View SolutionA proton of mass m and charge q is moving in a plane with kinetic energy E. if there exists a uniform magnetic field B, perpendicular to the plane motion. The proton will move in a circular path of radius
View SolutionA proton and an alpha particle projected with same velocity in uniform transverse magnetic field then
View Solution
