A circular disc is rotating with angular velocity ro. Aman standing at the edge walks towards the centre of disc. Then the angular velocity
decreases
increases
no change
halved
The correct Answer is:B
Apply law of.conservation of angular momentum.Angular momentum J = Iomega. When the man walks towards the centre of the disc from the edge, I decreases. Hence angular speed omega increases.
Similar Questions
A disc of radius R has a light pole fixed perpendicular to the disc at its periphery which in turn has a pendulum of length R attached to its other end as shown in figure. The disc is rotated with a constant angular velocity ω The string is making an angle 45∘ with the rod. Then the angular velocity ω of disc is

View SolutionA disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
View Solution
Knowledge Check
A disc of radius R has a light pole fixed perpendicular to the disc at its periphery whish in turn has a pendulum of legth R attached to its other end as shown in figure. The disc is rotated with a constant angular velocity ω The string is making an angle 45∘ with the rod. Then the angular velocity ω of disc is
 A(√3gR)1/2B(√3g2R)1/2C(g√3R)1/2D⎛⎜ ⎜⎝√2g(√2+1)R⎞⎟ ⎟⎠1/2
A(√3gR)1/2B(√3g2R)1/2C(g√3R)1/2D⎛⎜ ⎜⎝√2g(√2+1)R⎞⎟ ⎟⎠1/2A disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
ALinear momentumBAngular momentumCkinetic energyDMoment of inertiaA heavy disc is rotating with uniform angular velocity ω about its own axis. A piece of wax sticks to it. The angular velocity of the disc will
AincreaseBdecreaseCbecomes zeroDremain unchanged
A circular disc is rotating about its own axis at an angular velocity ω. If P is exact midpoint of dise between axis and rim of disc then angular velocity of Pis
View SolutionTwo discs of radii Rand2R are pressed against eachother. Initially, disc wit radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertiaof smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
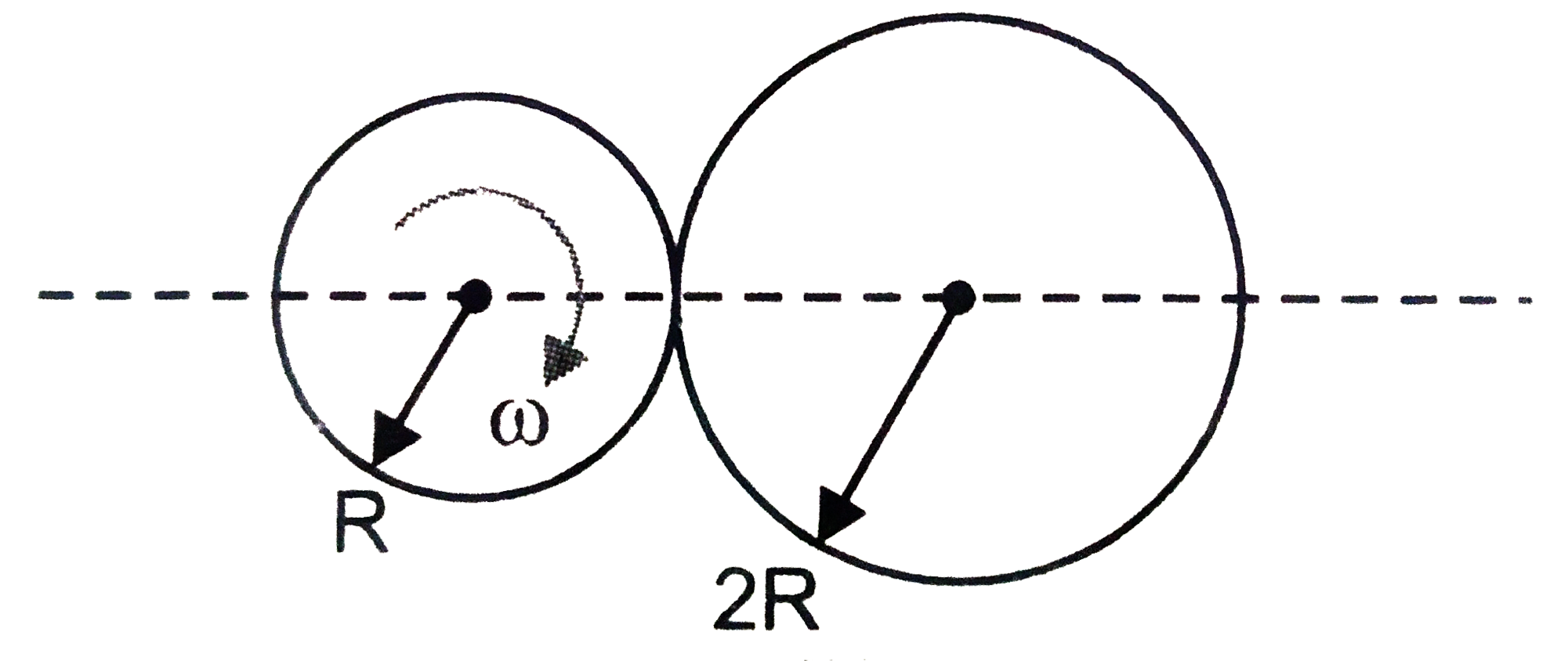
View SolutionTwo discs of radii Rand2R are pressed against each other. Initially, disc with radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertia of smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.

View SolutionA circular disc is rotating in horizontal plane about vertical axis passing through its centre without friction with a person standing on the disc at its edge. If the person gently walks to centre of disc then its angular velocity
View SolutionA disc rotates with angular velocity ω and kinetic energy E. Then its angular momentum
View Solution
