A uniform circular disc of radius R oscillates about a horizontal axis in its own plane. Find the distance of the axis from the centre, for the period to be maximum.
R2
R4
3R2
3R4
The correct Answer is:A
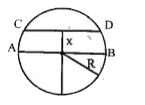
Let CD be the required axis at distance x from a dimater AB. CD is parallel to AB.
∵IAB=MR24∴ICD=MR24+Mx2 or MK2=M(R24+x2) K2=(R24+x2)
The time period will be maximum when K2x is minimum.
[For a compound pendulum, T=2π√K2+l2lg].
∴ For maximum T,K2x=(R24+x2)1x must be minimum therefoeddx(R24x+x)=0
or −R24x2+1=0 or x2=R2/4 or x=R/2
Similar Questions
An uniform disc is rotating at a constant speed in a vertical plane about a fixed horizontal axis passing through the centre of the disc. A piece of the disc from its rim detaches itself from the disc at the instant when it is at horizontal level with the centre of the disc and moving upwards, then about the fixed axis.
STATEMENT-1 : Angular speed of the disc about the aixs of rotation will increase.
and
STATEMENT-2 : Moment of inertia of the disc is decreased about the axis of rotation.
View SolutionA uniform circular disc of radius R oscillates in a vertical plane about a horizontal axis. Find the distance of the axis of rotation from the centre of which the period is minimum. What is the value of this period?
View Solution
Knowledge Check
A disc is made to oscillate about a horizontal axis passing through mid point of its radius. Determine time period.
A2π√3R2gB2π√2R3gC2π√RgD2π√2RgWhen a circular disc of radius 0.5 m is rotating about its own axis, then the direction of its angular momentum is
Aalong the tangent drawn at every pointBradialCperpendicular to the direction of angular velocityDalong the axis of rotation of the bodyA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to the plane with angular velocity ω. Another disc of same mass but half the radius is gently placed over it coaxially. The angular speed ofthe composite disc will be:
A5ω/4B4ω/5C2ω/5D5ω/2
A disc is made to oscillate about a horizontal axis passing through mid point of its radius. Determine time period.
View SolutionA uniform disc of radius R=13cm can rotate about a horizontal axis perpendicular to its plane and passing through the edge of the disc. Find the period of small oscillations of that disc if the logarithmic damping decrement is eqal to λ=1.00.
View SolutionThe mass of a thin circular plate is M and its radius is R. About an axis in the plane of plate at a perpendicular distance R/2 from centre of plate, its moment of inertia is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . Another disc of same dimensions but of mass 14 M is placed gently on the first disc co-axially. The angular velocity of the system is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . Another disc of same dimensions but of mass 14 M is placed gently on the first disc co-axially. The angular velocity of the system is
View Solution
