A coaxial line carries the same current i up the inside conductor of radius a as down the outer conductor of inner radius b and outer radius c. The magnetic induction field at distance r from the conductor.
The magnetic field at a distance r from the conductor when r<a is
μ04π⋅2ir2a2
μ04π⋅2ira2
μ04π⋅2i2r2a2
μ04π⋅2i(2)ra
The correct Answer is:B
When r<a, Consider a co-axial circular path of radius r. Let B be the magnitude of mag. field at this distance the B⋅2πrμ0× current enclosed by path
=μ0(iπa2×πr2)=μ0ir2a2 (using Ampere.s law) ∴B=μ04π×2ira2webermetre2
Similar Questions
A coaxial cable carries the a current i in the inside conductor of radius a as shown in figure-4.80 and the outer conductor of inner radius b and outer radius c carries a current i' in opposite direction. Find the magnetic induction due to the coaxial cable at distance r from the central axis of the cable for (a) r>a, (b) a<r<b and (c) b>r>c
 View Solution
View SolutionA current i ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor fo the cable, then the magnetic induction at any point outside the conductor at a distance r metre from the axis is
View Solution
Knowledge Check
- Question 1 - Select One
A current i ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor of the cable, then the magnetic induction at any point outside the conductor at a distance r meter from the axis is
A∞BZeroCμ04π2irDμ04π2πrr - Question 2 - Select One
Variation of magnetic field with distance from current carrying conductor is:
AB∝a2BB∝1a2CB∝aDB∝1a - Question 3 - Select One
A coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as
A B
B C
C D
D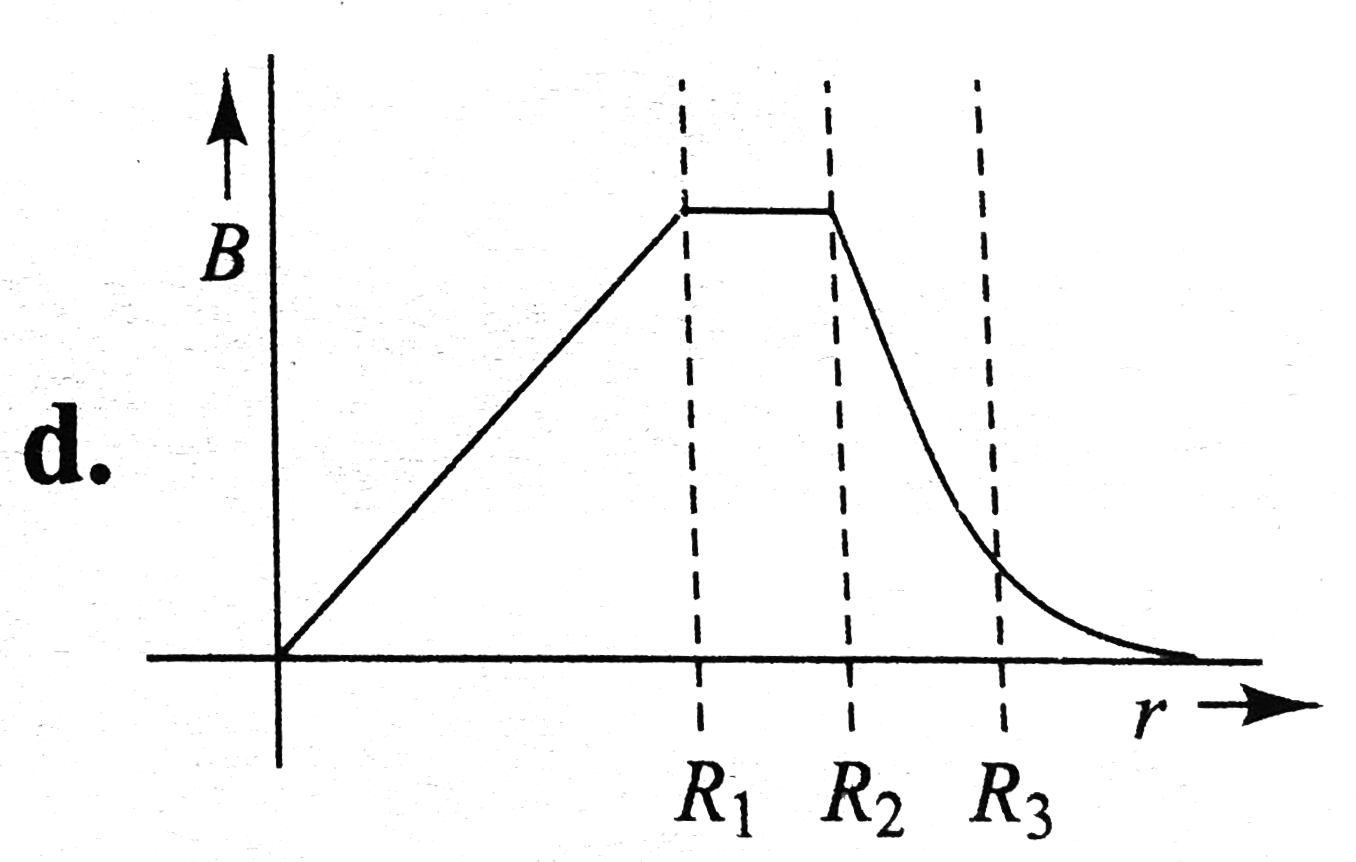
A coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as
View SolutionA coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as
View SolutionA coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as
View SolutionAmpere's law provides us an easy way to calculate the magnetic field due to a symmetrical distribution of current. Its mathemfield expression is ∮→B.dl=μ0Iin.
The quantity on the left hand side is known as line as integral of magnetic field over a closed Ampere's loop.
If the current density in a linear conductor of radius a varies with r according to relation J=kr2, where k is a constant and r is the distance of a point from the axis of conductor, find the magnetic field induction at a point distance r from the axis when rlta. Assume relative permeability of the conductor to be unity.View SolutionAmpere's law provides us an easy way to calculate the magnetic field due to a symmetrical distribution of current. Its mathemfield expression is ∮→B.dl=μ0Iin.
The quantity on the left hand side is known as line as integral of magnetic field over a closed Ampere's loop.
If the current density in a linear conductor of radius a varies with r according to relation J=kr2, where k is a constant and r is the distance of a point from the axis of conductor, find the magnetic field induction at a point distance r from the axis when rlta. Assume relative permeability of the conductor to be unity.View Solution
