You are provided with four identical cells each of emf 1.5V. How will you connect all of them to obtain a battery of emf 3V?
To obtain a battery of emf 3V using four identical cells each of emf 1.5V, we can follow these steps:
1. Understanding Series and Parallel Connections:
- When batteries are connected in series, their voltages add up. For example, if you connect two batteries of 1.5V in series, the total emf will be 1.5V + 1.5V = 3V.
- When batteries are connected in parallel, the voltage remains the same as that of a single battery, but the capacity (current) increases.
2. Determine the Configuration:
- We need to achieve a total emf of 3V using four 1.5V batteries. To do this, we can connect three batteries in series and one battery in reverse polarity.
3. Connect Three Batteries in Series:
- Connect the first battery (1.5V) to the second battery (1.5V) in series. Connect the positive terminal of the first battery to the negative terminal of the second battery.
- Now connect the third battery (1.5V) in series with the first two batteries. Connect the positive terminal of the second battery to the negative terminal of the third battery.
4. Connect the Fourth Battery in Reverse:
- Connect the fourth battery (1.5V) in reverse polarity. This means connecting the positive terminal of the fourth battery to the positive terminal of the first battery in the series and the negative terminal of the fourth battery to the negative terminal of the third battery in the series.
5. Calculate the Total emf:
- The total emf from the three batteries connected in series is:
V=1.5V+1.5V+1.5V−1.5V=3V
- The fourth battery, connected in reverse, effectively subtracts its voltage from the total.
6. Final Configuration:
- The final configuration will have three batteries adding up to 4.5V and one battery subtracting 1.5V, resulting in a total of 3V.
- When batteries are connected in series, their voltages add up. For example, if you connect two batteries of 1.5V in series, the total emf will be 1.5V + 1.5V = 3V.
- When batteries are connected in parallel, the voltage remains the same as that of a single battery, but the capacity (current) increases.
- We need to achieve a total emf of 3V using four 1.5V batteries. To do this, we can connect three batteries in series and one battery in reverse polarity.
- Connect the first battery (1.5V) to the second battery (1.5V) in series. Connect the positive terminal of the first battery to the negative terminal of the second battery.
- Now connect the third battery (1.5V) in series with the first two batteries. Connect the positive terminal of the second battery to the negative terminal of the third battery.
- Connect the fourth battery (1.5V) in reverse polarity. This means connecting the positive terminal of the fourth battery to the positive terminal of the first battery in the series and the negative terminal of the fourth battery to the negative terminal of the third battery in the series.
- The total emf from the three batteries connected in series is:
V=1.5V+1.5V+1.5V−1.5V=3V
- The fourth battery, connected in reverse, effectively subtracts its voltage from the total.
- The final configuration will have three batteries adding up to 4.5V and one battery subtracting 1.5V, resulting in a total of 3V.
Topper's Solved these Questions
- SAMPLE PAPER 2022BOOK - ICSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022EXERCISE - PART II (SECTION A)
12 Videos
- SAMPLE PAPER 2022BOOK - ICSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022EXERCISE - PART II (SECTION B)
8 Videos
- SAMPLE PAPER 2022BOOK - ICSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022EXERCISE - PART II (SECTION C)
8 Videos
Similar Questions
Three identical cells each of emf 2 V and internal resistance 1Ω are connected in series to form a battery. The battery is then connected to a parallel combination of two identical resistors, each of resistance 6Ω Find the current delivered by the battery.
View SolutionA battery is designed by connecting four cells, each of emf 1.5 V and resistance 2.0 ohm in parallel. If this battery is now connected to an resistance of 2.5 ohm, find
the potential drop across the terminal of the cells.
View SolutionA battery is designed by connecting four cells, each of emf 1.5 V and resistance 2.0 ohm in parallel. If this battery is now connected to an resistance of 2.5 ohm, find
the total resistance of the circuit
View SolutionA battery is designed by connecting four cells, each of emf 1.5 V and resistance 2.0 ohm in parallel. If this battery is now connected to an resistance of 2.5 ohm, find
the current flowing in the external circuit
View SolutionFour identical metal plates are arranged as shown plates 1 and 4 are connected by a connecting wire. A battery of emf V volts is connected between plates 2 and 3. The electric field between plates 3 and 4 is 2VKd. Find the value of K

View SolutionThree identical cells, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View SolutionFour identical cells each of emf 2V, are joined in parallel providing supply of current to external circuit consisting of two 15Ω resistors joined in parallel. The terminal voltage of the cells ae read by an ideal voltmeter is 1.6V. Calculate the internal resistance of each cell.
View SolutionThere are ten identical cells each of emf 10V and internal resistance 0.25 Ω are short circuited as shown in figure. The value of potential difference (Vx−Vy)is
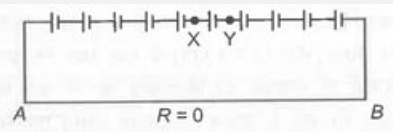
View SolutionFive identical capacitor plates are arranged such that they make four capacitors each of 2μF. The plates are connected to a source of emf 10V. The charge on plate C is

View Solutioncells each of emf e and internal resistance r are joined in series to form a row and such rows are connected in parallel to form a battery of N = mn cells. If this battery is connected to an external resistance R.
What is the emf of this battery and how much is its internal resistance ?
View Solution
