ABCD is a trapezium with AB parallel to DC and DC = 3AB. M is the mid-point of DC, ¯¯¯¯¯¯AB=¯p and ¯¯¯¯¯¯BC=¯q. Find the terms of ¯p and ¯q.
¯¯¯¯¯¯¯AM
Text Solution
The correct Answer is:¯b−12¯a
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
If D is the mid -point of side AB of ΔABC, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AC=
A2(¯¯¯¯¯¯AD−¯¯¯¯¯¯BD)B2(¯¯¯¯¯¯DC−¯¯¯¯¯¯BD)C2(¯¯¯¯¯¯BD−¯¯¯¯¯¯CA)D2(¯¯¯¯¯¯BD−¯¯¯¯¯¯AC) - Question 2 - Select One
If ABCDE is a pentagon, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯AE+¯¯¯¯¯¯BC+¯¯¯¯¯¯DC+¯¯¯¯¯¯ED=
A¯¯¯¯¯¯ACB2¯¯¯¯¯¯ACC2¯¯¯¯¯¯ADD3¯¯¯¯¯¯AD - Question 3 - Select One
If ABCD is a square, then
¯¯¯¯¯¯AB+2¯¯¯¯¯¯BC+3¯¯¯¯¯¯CD+4¯¯¯¯¯¯DA =A4 ¯¯¯¯¯¯ACB3 ¯¯¯¯¯¯ACC2 ¯¯¯¯¯¯CAD¯¯¯¯¯¯AC
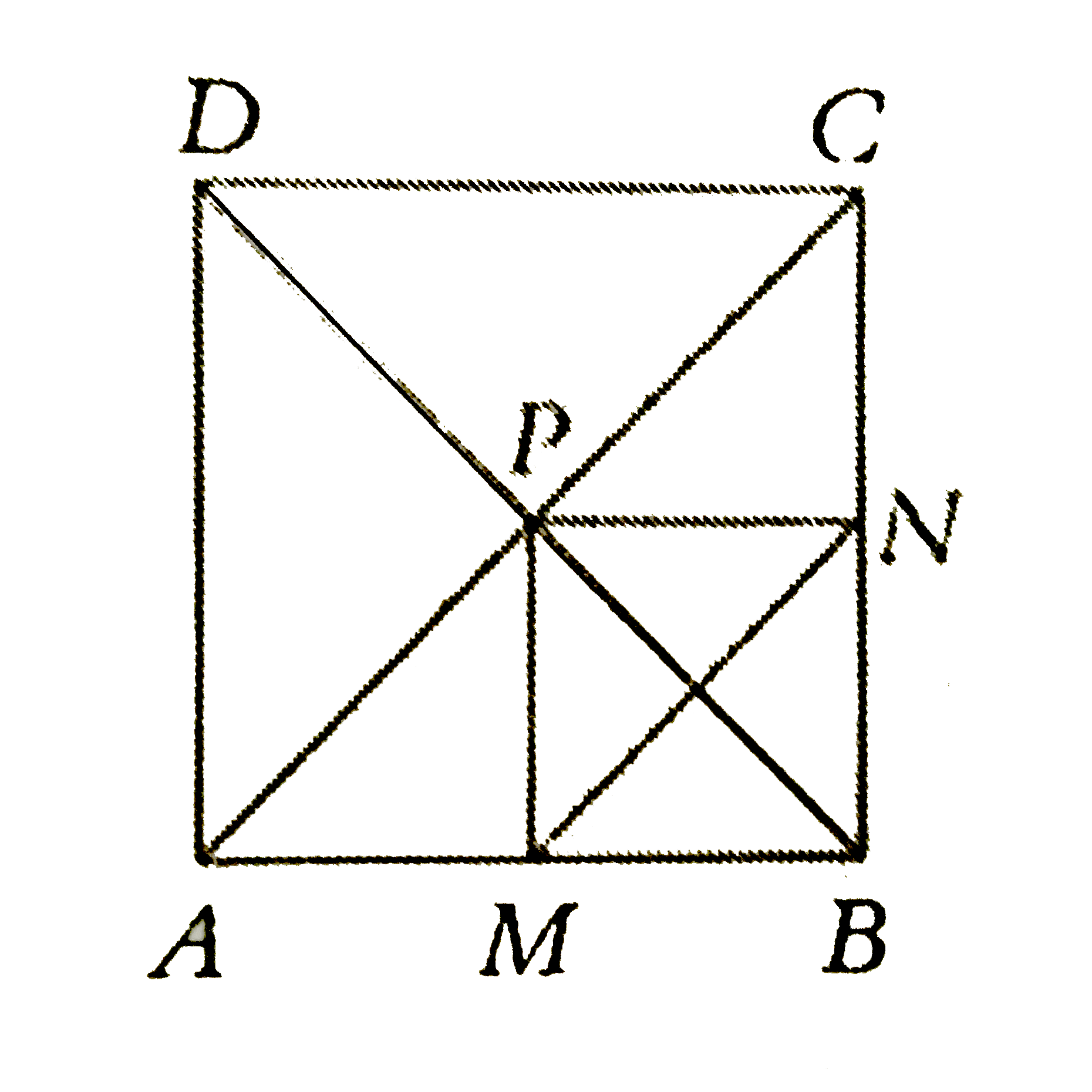
In the figure above, ABCD is a square of side 18 cm and ¯¯¯¯¯¯PN⊥¯¯¯¯¯¯BCand¯¯¯¯¯¯¯PM⊥¯¯¯¯¯¯AB. Find the length of MN.View SolutionABCDE is a regular hexagon. i) If ¯¯¯¯¯¯AB+¯¯¯¯¯¯AE+¯¯¯¯¯¯BC+¯¯¯¯¯¯DC+¯¯¯¯¯¯ED+¯¯¯¯¯¯AC=λ¯¯¯¯¯¯AC then λ=
View SolutionFind m∠C in the given figure if ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯DC.
View Solution-
In the figure above, ABCD is a square of side 18 cm and ¯¯¯¯¯¯PN⊥¯¯¯¯¯¯BCand¯¯¯¯¯¯¯PM⊥¯¯¯¯¯¯AB. Find the length of MN.View Solution In △ABC,∠B=90∘, P,Q and R are the mid-points of ¯¯¯¯¯¯AB,¯¯¯¯¯¯BC and ¯¯¯¯¯¯AC respectively. Then which of the following is true?
View Solution