In a trapezium ABCD, AB = CD, if OA = x - 4, OB = 3x - 19, OC = 4 and 0D . = x - 3, find x, where O is the meeting point of its diagonals .
10 units
9 units
no other is correct
12 units
The correct Answer is:D
Similar Questions
In Fig. AB∣∣CD . If OA=3x−19, OB=x−4 , OC=x−3 and OD=4 , find x .
View SolutionIn parallelogram ABCD , AB = (3x- 4) cm, BC = ( y- 1) cm , CD = ( y+ 5) cm and AD = (2x+ 5) cm. find the ratio AB : BC.
Find the values of x and y.
View SolutionIn Fig. 4.72, ABCD . If OA=3x−19, OB=x−4 , OC=x−3 and OD=4 , find x . (FIGURE)
View Solution13. In parallelogram ABCD, AB=2x+7,BC=4x−5,CD=3x−8. Find the perimeter of the parallelogram.
View SolutionIf ABCD is a square. X is a point on CD, such that DX = DO. Find ∠DOX∠XOC. O is the intersection point of diagonals.

View SolutionABCD is a trapezium . AB ||CD and AB:CD=5:4, E and F are mid points of AD and BC, if CD= 20 cm , Find EF
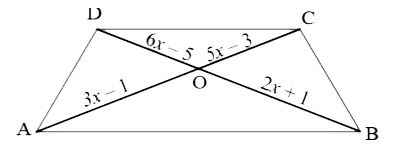
View SolutionIn the given fig., AB || DC and diagonals AC and BD intersects at O. If OA =3x-1 and OB =2x + 1, OC = 5x-3 and OD =6x-5, find the value of x.
View SolutionIn a given figure in trapezium ABCDifAB∣∣CD then value of x is :
View SolutionDiagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
View SolutionDiagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
View Solution
