If ABCD is a square. X is a point on CD, such that DX = DO. Find ∠DOX∠XOC. O is the intersection point of diagonals.

The correct Answer is:31
Step by step video & image solution for If ABCD is a square. X is a point on CD, such that DX = DO. Find (angleDOX)/(angleXOC). O is the intersection point of diagonals. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - QUADRILATERALEXERCISE - EXERCISE
48 Videos
- PROFIT & LOSSBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - PROFIT & LOSSEXERCISE - Questions
200 Videos
- RATIO & PROPORTIONBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - RATIO & PROPORTIONEXERCISE - QUESTIONS
113 Videos
Similar Questions
Knowledge Check
A Tank is normally filled in 9 hours but takes four hours longer to fill because of a leak in its bottom. If the tank is full, the leak will empty it in ?
AA) 32.5 hrsBB) 29.25 hrsCC) 30.30 hrsDD) 31 hrsABCD is a trapezium in which AB∣∣CD and AB=2CD. It its diagonals intersect each other at O then ratio of the area of triangle AOB and COD is
A1:2B2:1C4:1D1:4Let ABCD be a square and let P be point on segment CD such that DP : PC = 1 : 2. Let Q be a point on segment AP such that ∠BQP=90∘. Then the ratio of the area of quadrilateral PQBC to the area of the square ABCD is
A3160B3760C3960D4160
If ABCD is a quadrilateral whose diagonals AC and BD intersect at O, then

View SolutionTwo lines AB and CD intersect at a point O such that ∠BOC+∠AOD=280∘, as shown in the figure. Find all the four angles.
View SolutionAB is a diameter of the circle. Two points C and D are such point that CD = BD. AB and CD intersect at O. If angle ∠AOD=45∘. Find ∠ADC
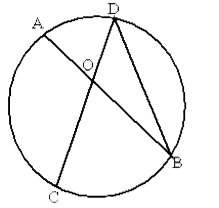
View SolutionThere are two circular flower beds on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.
View SolutionThe point of intersection of diagonals of a square ABCD is at the origin and one of its vertices is at a(4,2). What is the equation of the diagonal BD?
View Solution
