If F denotes the contact force, f denotes the frictional force exerted by one surface on the other, FN denotes the normal reaction force between the two respectively and none of them are zero, then
F<f
FN<F
FN>F
FN−f<F<FN+f
To solve the problem, we need to understand the relationship between the contact force (F), the frictional force (f), and the normal reaction force (F_N). Here’s the step-by-step solution:
Step 1: Understand the Forces Acting on the Object
When an object is placed on a surface and a force is applied to it, there are three primary forces to consider:
- The normal reaction force (F_N), which acts perpendicular to the surface.
- The frictional force (f), which opposes the motion of the object.
- The contact force (F), which is the resultant force acting on the object.
Step 2: Identify the Relationship Between the Forces
According to the given information:
- The net contact force (F) can be represented as a vector sum of the normal reaction force (F_N) and the frictional force (f).
- This can be mathematically expressed using the Pythagorean theorem since the normal force and frictional force act at right angles to each other.
Step 3: Apply the Pythagorean Theorem
The relationship can be expressed as:
F=√F2N+f2
This equation shows that the net contact force (F) is the hypotenuse of a right triangle formed by the normal force (F_N) and the frictional force (f).
Step 4: Analyze the Magnitudes of the Forces
Since none of the forces are zero, we can conclude that:
- The net contact force (F) is greater than both the normal reaction force (F_N) and the frictional force (f).
- Specifically, since F is the resultant of F_N and f, it must be greater than either of the individual forces.
Step 5: Conclusion
From the analysis, we can conclude that:
F>FN
and
F>f
Thus, the net contact force (F) is greater than both the normal reaction force (F_N) and the frictional force (f).
Final Statement
Therefore, the correct conclusion is that the net contact force (F) is greater than the normal reaction force (F_N) and the frictional force (f).
---
When an object is placed on a surface and a force is applied to it, there are three primary forces to consider:
- The normal reaction force (F_N), which acts perpendicular to the surface.
- The frictional force (f), which opposes the motion of the object.
- The contact force (F), which is the resultant force acting on the object.
According to the given information:
- The net contact force (F) can be represented as a vector sum of the normal reaction force (F_N) and the frictional force (f).
- This can be mathematically expressed using the Pythagorean theorem since the normal force and frictional force act at right angles to each other.
The relationship can be expressed as:
F=√F2N+f2
This equation shows that the net contact force (F) is the hypotenuse of a right triangle formed by the normal force (F_N) and the frictional force (f).
Since none of the forces are zero, we can conclude that:
- The net contact force (F) is greater than both the normal reaction force (F_N) and the frictional force (f).
- Specifically, since F is the resultant of F_N and f, it must be greater than either of the individual forces.
From the analysis, we can conclude that:
F>FN
and
F>f
Thus, the net contact force (F) is greater than both the normal reaction force (F_N) and the frictional force (f).
Therefore, the correct conclusion is that the net contact force (F) is greater than the normal reaction force (F_N) and the frictional force (f).
Topper's Solved these Questions
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - CONSOLIDATED EXERCISE.
1 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - CONSOLIDATED EXERCISE. (MULTIPAL-CHOICE QUESTION WITH ONE OR MORE THAN ONE CORRECT ANSWER)
3 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES (Read the given statements and select the correct option.)
1 Videos
- ELASTICITYBOOK - CENGAGE PHYSICSCHAPTER - ELASTICITYEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
- SOUNDBOOK - CENGAGE PHYSICSCHAPTER - SOUNDEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISE
10 Videos
Similar Questions
The angle between the resultant contact force and the normal force exerted by a body on the other is called the angle of friction. Show that it λ be the angle of friction and μ the coefficient of static friction. λ≤tan−1μ.
View SolutionAnalysis Of Friction Force Between Two Objects In Contact
View Solution
Knowledge Check
Suppose F,FN&f are the magnitudes of the contact force, normal force and the frictional force exerted by one surface on the other, kept in contact, if none of these is zero :
AF>fBFN>fCF>FND(FN−f)<(FN+f)Let F,FNandf denote the magnitudes of the contact force, normal force and the friction exerted by one surface on the other kept in contact. If none of these is zero,
AF>FNBF>1CF_NgtfDFN−f<F<FN+f.The contact force exerted by a body A on another body B is equal to the normal force between the bodies. We concude that
Athe surface must be frictionlessBthe force of friction between the bodies is zeroCthe magnitude of normal force equals that of frictionDthe bodies may be rough but they don't slip on each other.
Calculate F such that frictional force acting on all blocks zero.
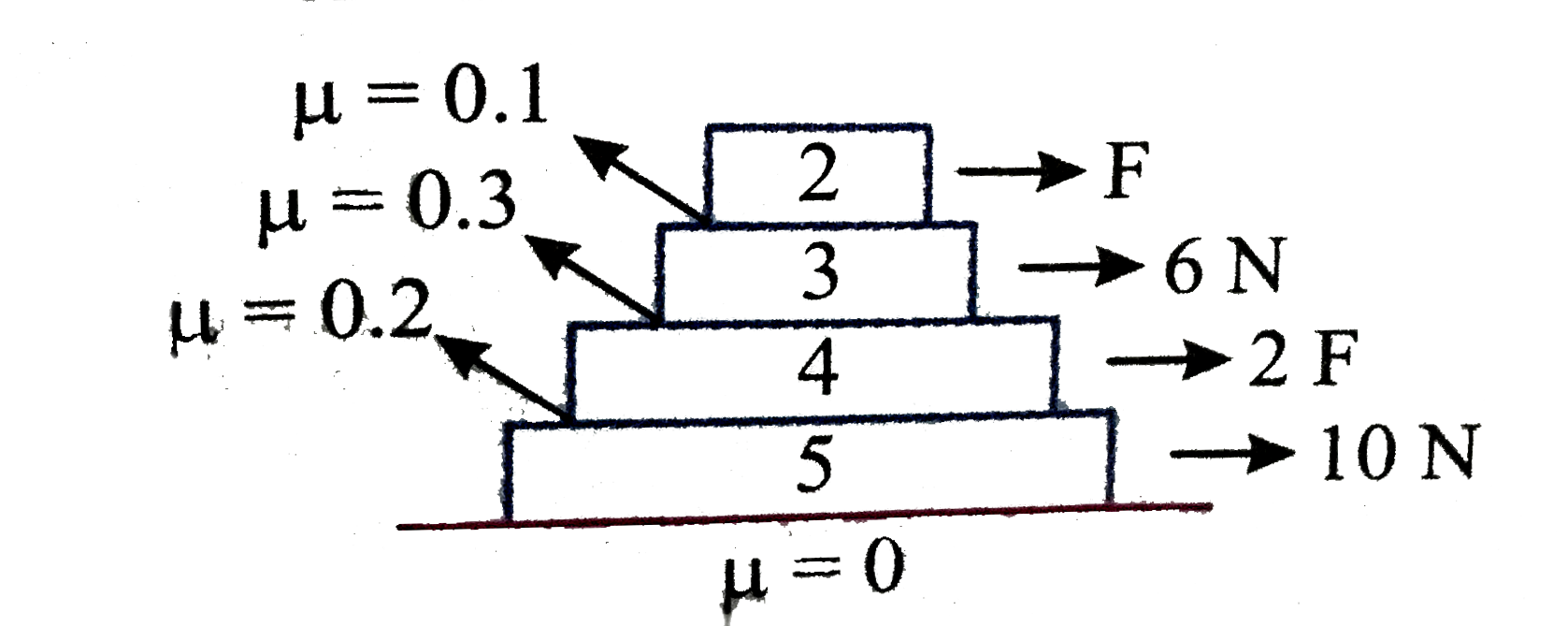
View SolutionExplain why two surfaces in contact with each other experience frictional force.
View SolutionTwo blocks are kept in contact as shown in figure. Find ( a) forces exerted by surfaces ( floor and wall ) on blocks ( b) contact force between two blocks.
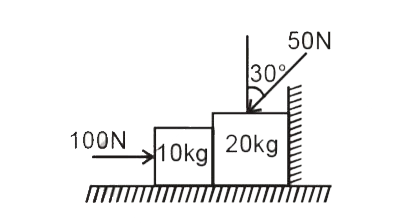
View SolutionIf x,F and U denote the dispalcement, force acting on and potential energy of a particle then
View SolutionLet F1 be the magnitude of the gravitational force exerted on the Sun by Earth and F2 be the magnitude of the force exerted on Earth by the Sun. Then:
View Solution
