E and F are points on diagonals AC of a parallelogram ABCD such that AE=CF. show that BFC parallelogramSolution in Punjabi
Step by step video & image solution for E and F are points on diagonals AC of a parallelogram ABCD such that AE=CF. show that BFC parallelogram by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Three angles of a quadrilteral are respectively 50∘ and 110∘ and 100∘ . Find the fourth angles.
View SolutionDefine a trial.
View SolutionDefine
Statistics as a subject.
View SolutionABCD is a Parallelogram. AE is perpendicular on DC and CF is perpendicular on AD. If AB= 10cm, AE = 8cm, CF =12cm . Find AD ?
View SolutionABCD is a parallelogram. E is a point on BA such that BE =2 EA and F is a point on Do such that DF=2 FC. Prove that AE CF is a parallelogram whose area is one third area of parallelogram AB CD
View SolutionPoint E and F lie on diagonals AC of a parallelogram ABCD such that AnE=CF. What type of quadrilateral is BFDE? From the given figure we see that BFDEis also a parallelogram.
View SolutionABCD एक समानान्तर चतुर्भुज है तथा विकर्ण AC,BD एक –दूसरे को बिंदु O पर काटते हैं। यदि E,F,F तथा H,AO,DO,CO तथा BO के मध्य बिंदु हैं। चतुर्भुज EFGH के परिमाप तथा समानान्तर चतुर्भुज ABCD के परिमाप का अनुपात ज्ञात करें?
View SolutionE and F are points on diagonal AC of a parallelogram ABCD such that AE=CF. Show that BFDE is a parallelogram.
View SolutionABCD is a parallelogram and E is a point, on BC. If the diagonal BD intersects AE at F, prove that AF×FB×EF×FD.
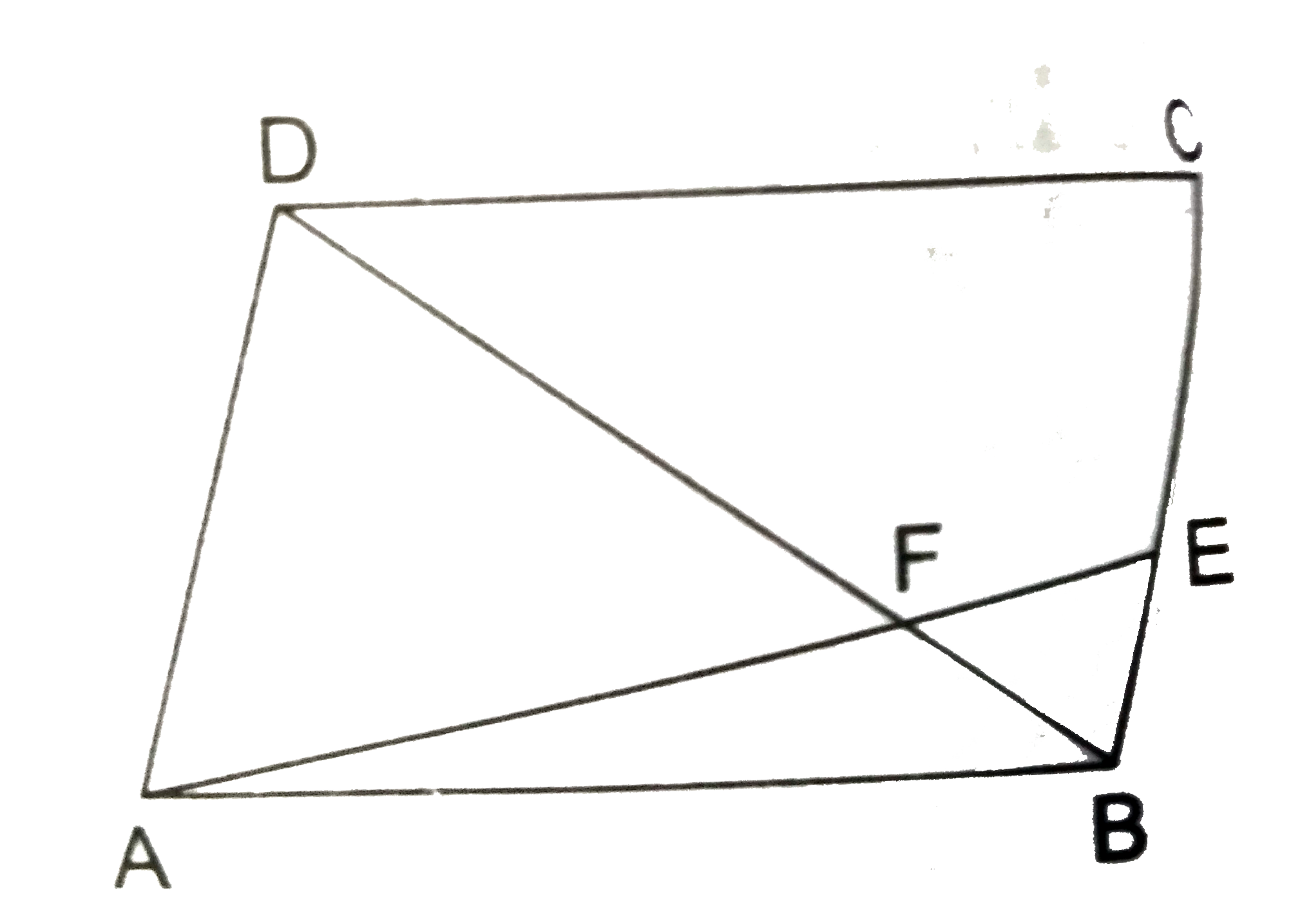
View Solutionबगल के चित्र में समान्तर चतुर्भुज ABCD का विकर्ण BD रेखा खण्ड AE को F बिन्दु पर प्रतिच्छेद करता है , जहाँ E,BC भुजा पर कोई बिन्दु है । दिखाएँ कि DF×FE=BF×FA.
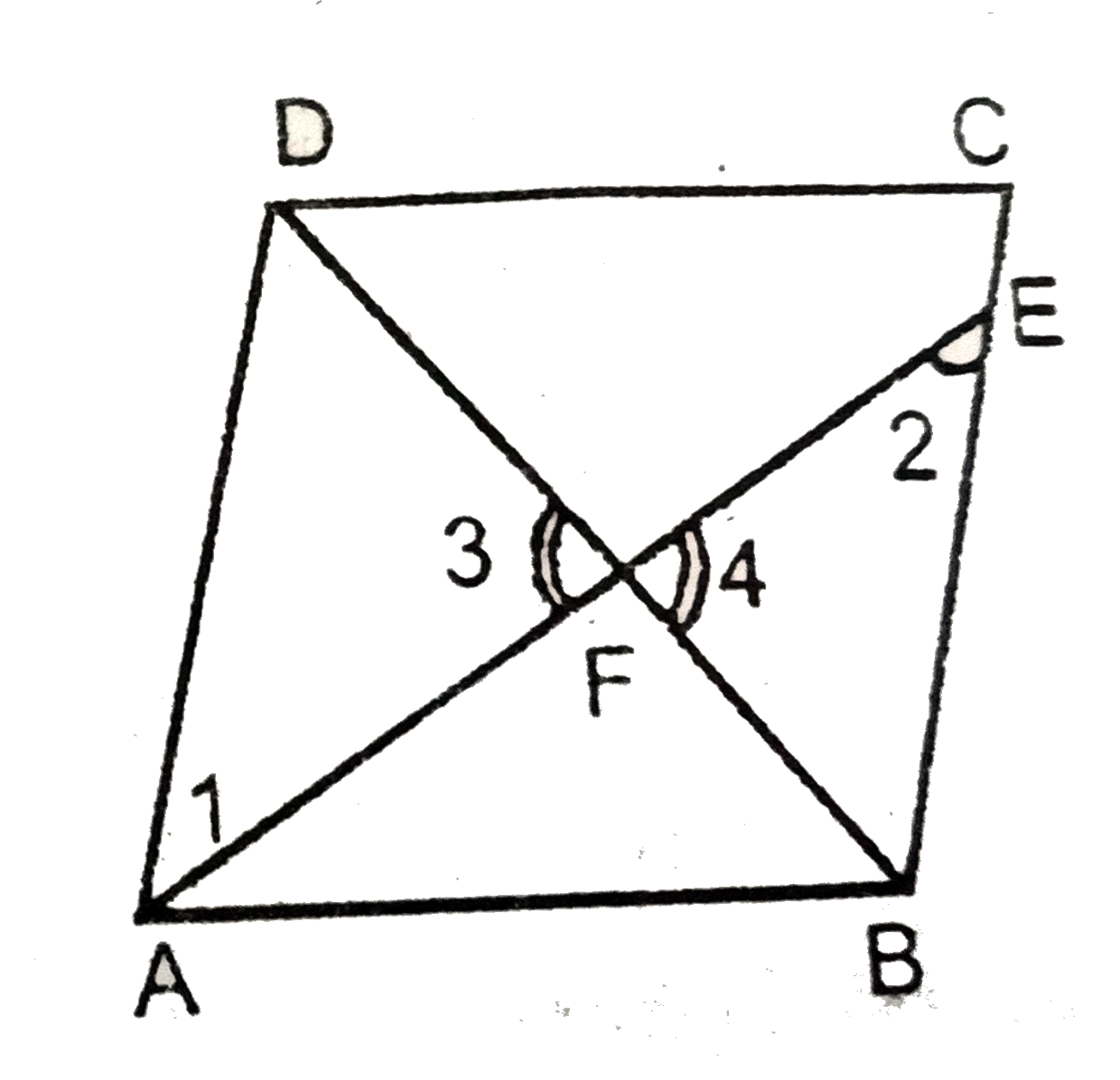
View SolutionABCD एक समांतर चतुर्भुज है और रेखाखण्ड AE एवं CF क्रमशः ∠A और ∠C को समद्विभाजित करते हुए CD से E पर तथा AB से F पर मिलते हैं। दिखाइए कि AE∣∣EF
View SolutionE तथा F किसी समांतर चतुर्भुज ABCD की भुजाओ DC तथा AD पर स्थित दो बिंदु है । दिखाइए कि ar(AEB)=ar(BFC).
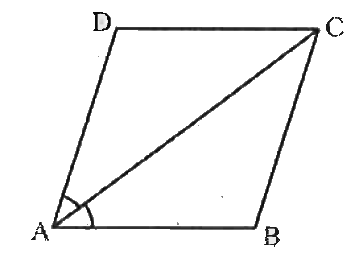
View SolutionDiagonal AC of a parallelogram ABCD bisects A. Show that
ABCD is a rhombus.
View SolutionAC is a common diagonal to both the parallelograms ABCD and AECF. If the points B , E , D , F are not collinear , prove that BEDF is a parallelogram.
View SolutionIn the adjacent figure , ABCD is a parallelogram and line segments AE and CF bisect the angles A and C respectively . Show that AE∣∣CF.
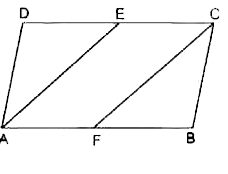
View SolutionABCD एक समांतर चतुर्भुज है जिसके विकर्ण E बिंदु प्रतिच्छेद करते है। AC को F तक इस तरह बढाया गया हैं कि CF = AE सिध्द कीजिए। कि ar (ΔBDF)=ar(∣∣gmABCD)
View Solution
