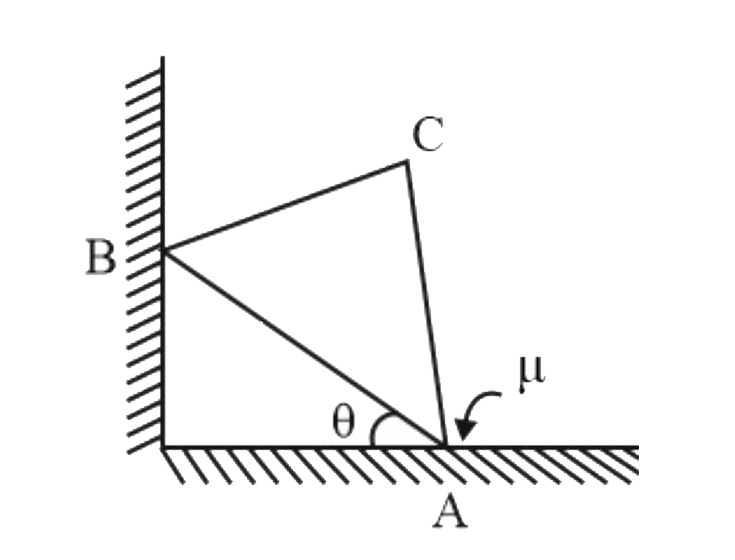
A uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction $μ$ and its upper end against a smooth vertical wall. If $θ$ is the inclination of the ladder with the wall, then $θ$ is equal to

${tan}^{- 1} μ$

${cot}^{- 1} μ$

${cot}^{- 1} (2 μ)$

${tan}^{- 1} (2 μ)$

Text Solution

Verified by Experts

The correct Answer is:D

A uniform ladder rests in limiting equilibrium, its lower end on a rough horizontal plae and its upper end against a smooth vertical wall. If $θ$ is the engle of inclination of the ladder to the vertical wall and $μ$ is the coefficient of friction then $tan θ$ is equal to
A $μ$
B $2 μ$
C $3 μ / 2$
D $μ + 1$
A rod of length I leans by its upper end against a smooth vertical wall, while its other end leans against the floor. The end that leans against the wall moves uniformly downward. Then:

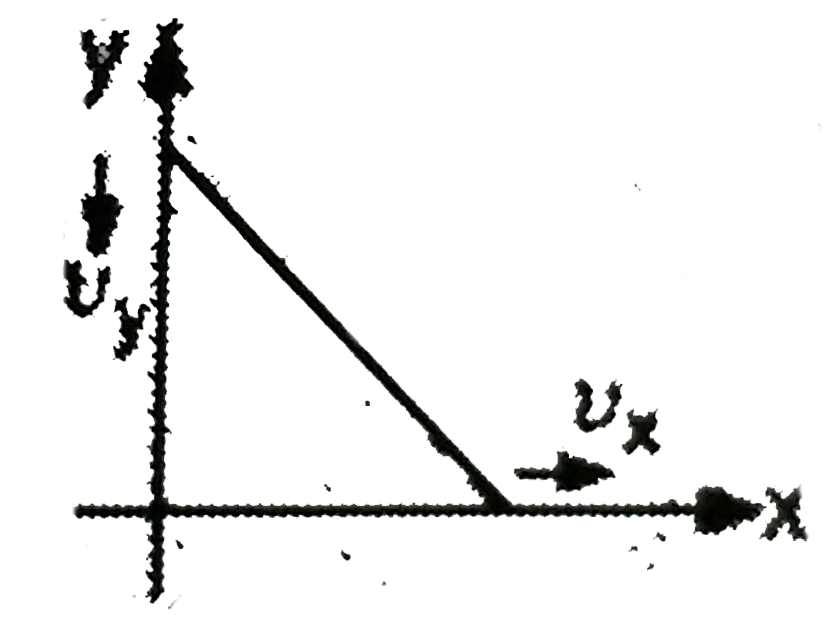AThe other end also moves uniformly
BThe speed of other end goes on decreasing
CThe speed of other end goes on increasing
DThe speed of other end first decreases and then increases