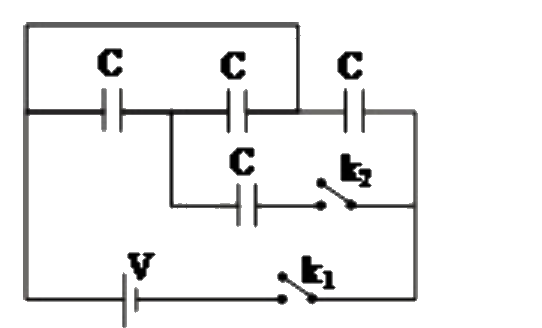
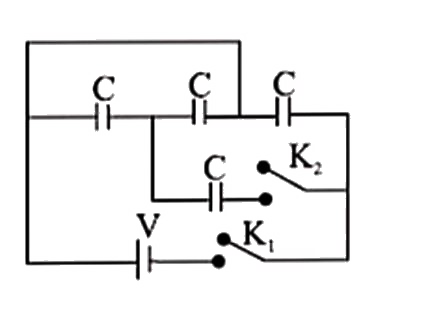
Initially K1 is closed, now if K2 is also closed, find heat dissipated in the resistances of connecting wires
12CV2
23CV2
13CV2
14CV2
The correct Answer is:C
When K1 is closed upper circuit is connected to source
Q = CV
Energy U1=12CV2
When K2 is also closed complete circuit is connected to source.
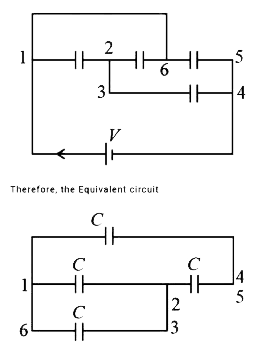
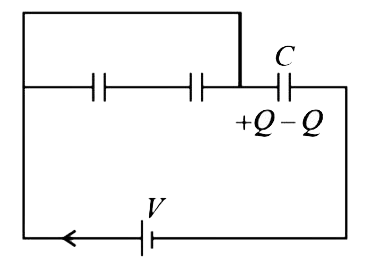
Therefore, the Equivalent circuit
Cequi=C+2C3=5C3
Uf=125C3V2=5C6V2
Charge supplied by battery after closing K2 is
Q=53CV−CV=23CV
Energy supplied by battery =Uf−Ui+H
23CV2=56CV2−12CV2+H
H=13CV2
Topper's Solved these Questions
Similar Questions
Knowledge Check
Initially K1 is closed, now if K2 is also closed, find heat dissipated in the resistances of connecting wires
 A12CV2B23CV2C13CV2D14CV2
A12CV2B23CV2C13CV2D14CV2The capacitor 'C' is initially unchanged. Switch S1 is closed for a long time while S2 remains open. Now at t=0S2 is closed while S1 is opened. All the batteries are ideal and connecting wires are resistanceless
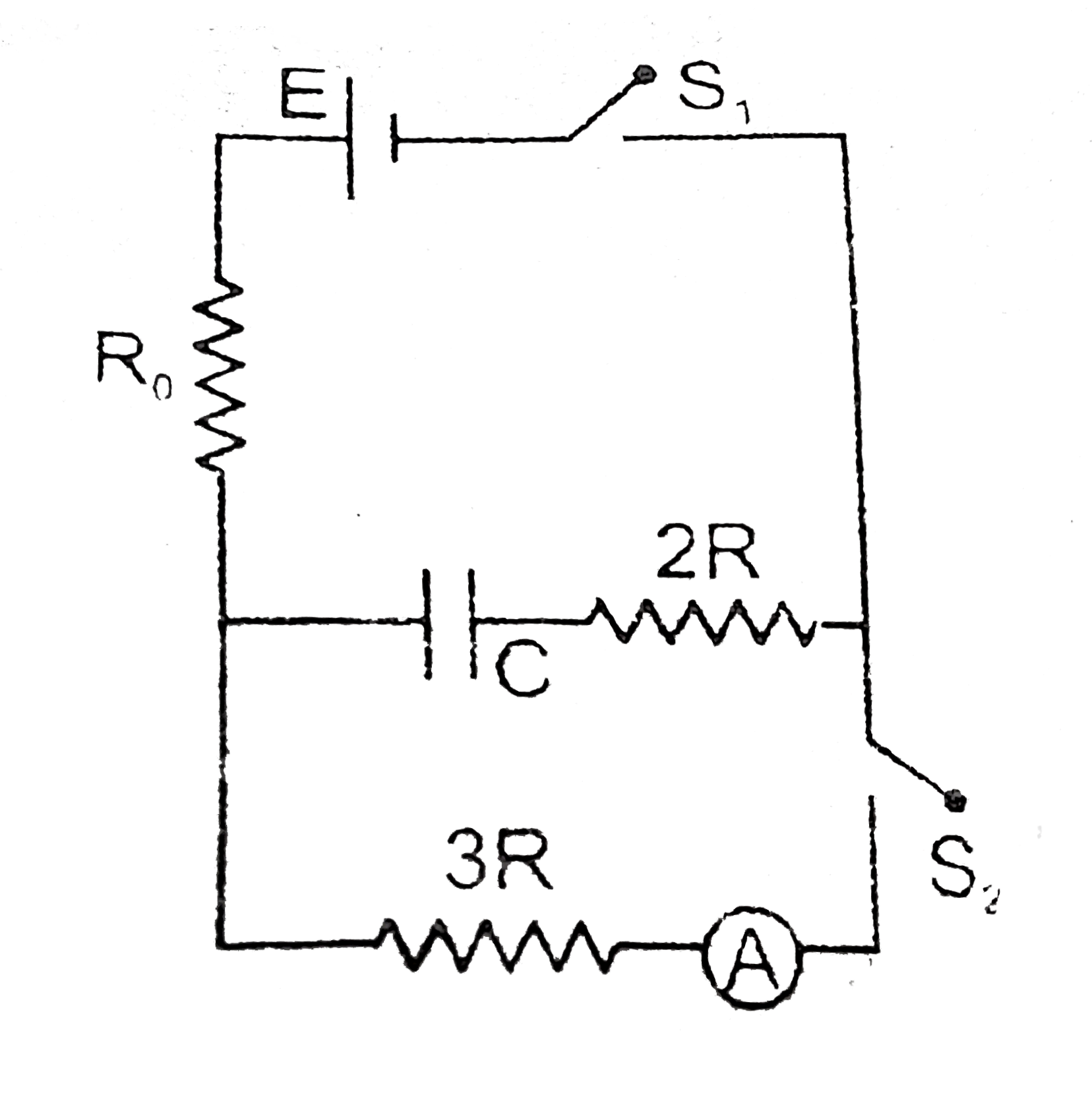 AAt time t = 0, reading of ammeter is E5RBAt time t =0, reading of ammeter is zeroCHeat developed till time t=5RCln2 in resistance 3 R is 940CE2DAfter time t>0 charge on the capacitor follows the equation CEe−t/5RC
AAt time t = 0, reading of ammeter is E5RBAt time t =0, reading of ammeter is zeroCHeat developed till time t=5RCln2 in resistance 3 R is 940CE2DAfter time t>0 charge on the capacitor follows the equation CEe−t/5RCIn the circuit shown in figure , initially key K1 is closed and key K2 is open. Then K1 is opened and K2 is closed (order is important). [Take Q′1 and Q′2 as charges on C1 and C2 and V1 and V2 as voltage respectively].
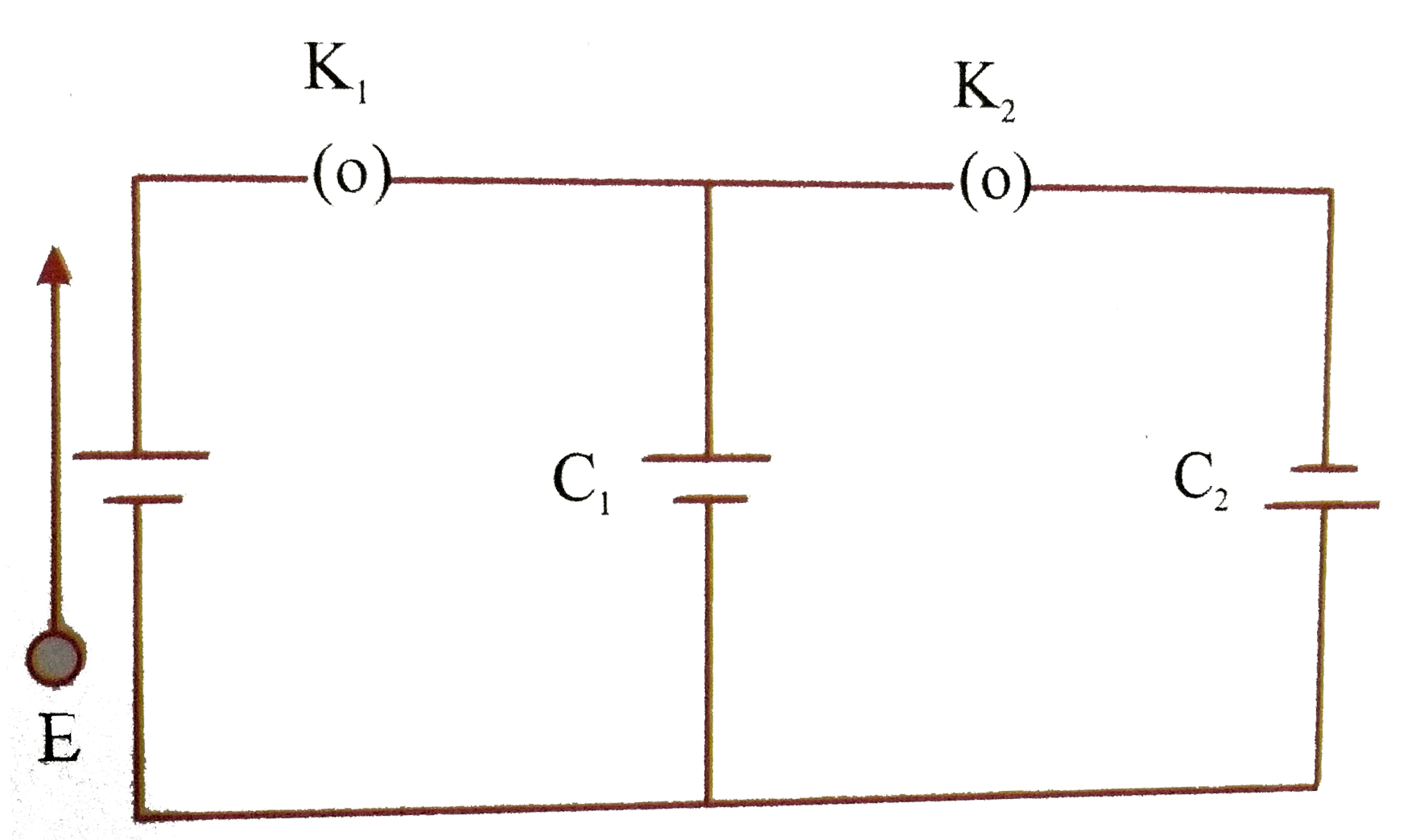
ThenAcharge on C1 gets redistributed such that V1=V2Bcharge on C1 gets redistributed such that Q′1=Q′2Ccharge on C1 gets redistributed such that C1V1+C2V2=C1EDcharge on C1 gets redistributed such that Q′1+Q′2=Q.
The reading of an ammeter in the circuit
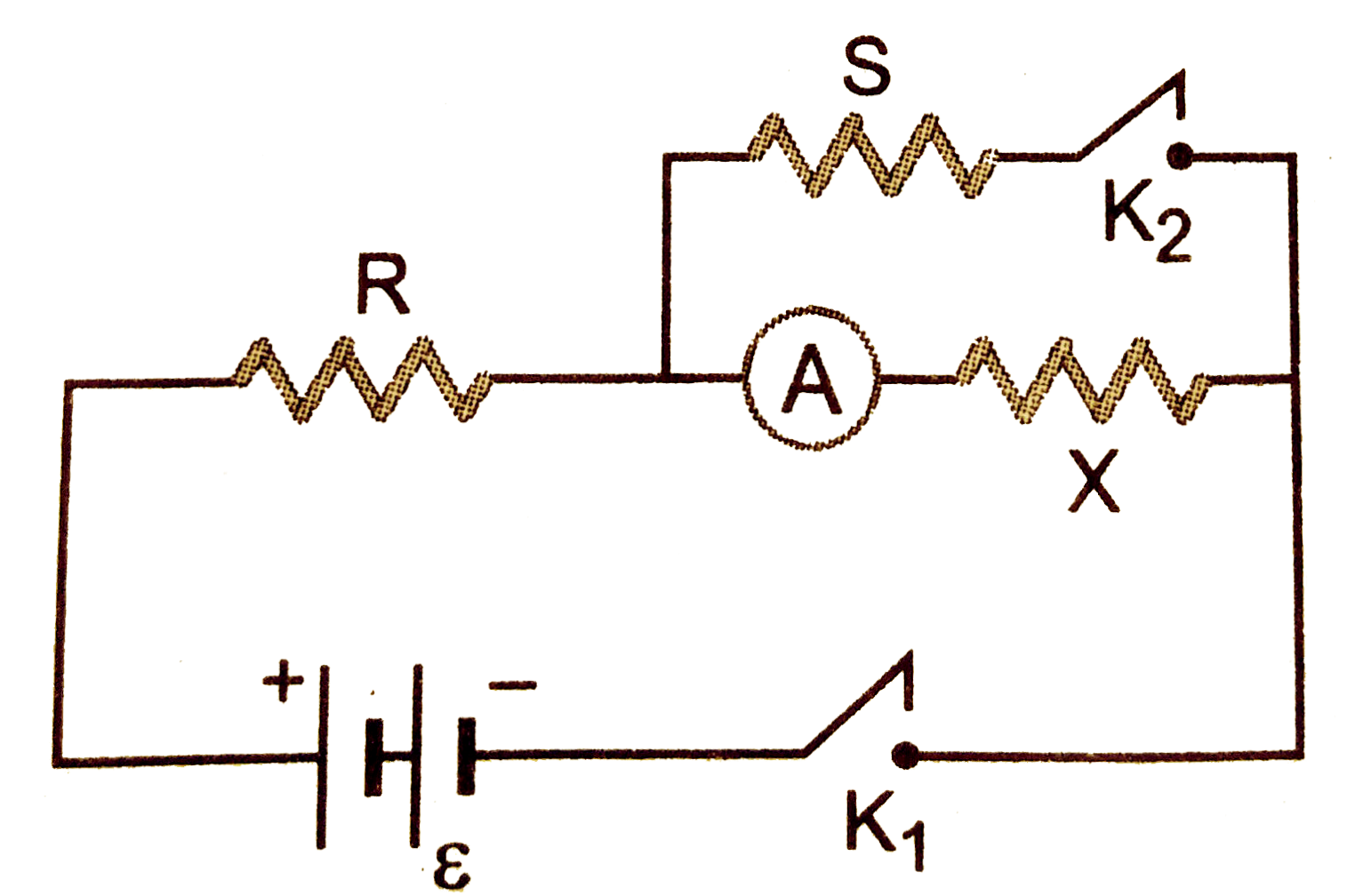
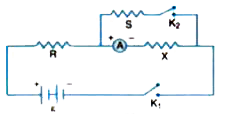
(i) I when key K1 closed key K2 is open
(ii) I/2 when both keys K1andK2 are closed Find the expression for the resistance of X in terms of the resistances of R and S
View SolutionIn the circuit shown in Fig, instially K1 is closed and K2 is open . What are the charges on each capacitor.
Then K1 was opened and K2 was closed (order is important). What will be the charge on each capacitor now ? [C=1μF]
View SolutionIn the circuits shows in S1 and S2 are switches. S2 remains closed for a long time and S1 is opened. Now S1 is also closed. Just after S1 is closed, find the potential difference (V) across R and di/dt (with sign) in L.

View SolutionThe reading of an ideal ammeter, in the circuit shown here, equals (i) I when key K1 is closed but key K2 is open , (ii) I2 when both keys K1 and K2 are closed. Find the expression for the resistance of X in terms of the resistance R and S.
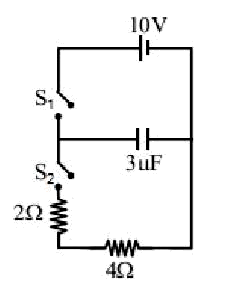
View SolutionIn given circuit initially switch S1 is closed for long time and then opened and now S2 is closed. The total energy dissipated in 4Ω resistor is equal to :-
View Solution